CENNO SUI NUMERI PRIMI^[1]

I numeri primi, nonostante la loro apparente semplicità, rappresentano uno dei più difficili e nello stesso tempo affascinanti argomenti dell’intera matematica pura. Una volta fissata la loro definizione (numeri divisibili solo per l’unità e per loro stessi) e stabilito che i numeri interi o sono primi oppure sono dati dal prodotto di numeri primi (cosicché questi primi vengono definiti i “mattoni” su cui sono costituiti tutti i numeri) è possibile stabilire alcune tappe fondamentali del loro studio che per ora ci limitiamo solo ad elencare trascurando, per nostra incompetenza, il legame con la musica che taluni considerano assai stretto (per questo si veda ad es, [1] pp. 171-179).

Prima di iniziare ricordiamo una circostanza relativa ai numeri primi rimasta tuttora inspiegabile: nel 1960 ad opera dell’esploratore e geologo  Jean  de Heinzelin è stato trovato ad Ishango, nei pressi del lago Edoardo, tra l'Uganda e il Congo,. un osso di babbuino (datato tra il 18 000 e il 20 000 a. C.) sul quale si trovano incise tre serie di numeri una delle quali costituita dai numeri primi 11; 13; 17; 19. ([1_a], p, 40).

Sono state avanzate molte ipotesi per spiegare  le tre successioni e quella in particolare dei numeri primi ma non riteniamo significativo riportarle. Rimane comunque il mistero della presenza della serie dei numeri primi in un’epoca così antica.

Lasciando irrisolta la presenza dei quattro “mattoni” scritti come si è visto di seguito, possiamo sintetizzare questo lavoro sui numeri primi in sei punti senza presumere di aver indicato tutte le proprietà raggiunte sull’argomento anche se esse appaiono le principali.

1. I numeri primi sono infiniti;
2. È possibile determinare intervalli numerici grandi a piacere privi di numeri primi;
3. Sono state fatte varie ipotesi sulla distribuzione dei numeri primi e su alcune loro proprietà ma senza ottenere una formula generale che permettesse di calcolare la loro successione completa;
4. L’ipotesi di Gauss dà una certa indicazione sulla distribuzione dei numeri primi;
5. Sulla scorta della indicazione di Gauss e sullo sviluppo della serie armonica, sviluppata da Eulero e poi da Riemann si giunge ad una congettura notevole verificata per milioni di casi ma mai dimostrata;
6. Il mistero dei numeri primi è incredibilmente legato al mistero del nostro cervello. La circostanza è assolutamente sconvolgente

Prima di sviluppare i sei punti elencati sopra, osserviamo una caratteristica di questi numeri che talvolta sono separati da un solo numero (pari). In tal caso tale coppia viene indicata con coppia di numeri “primi gemelli” (nell’ultima riga del nostro elenco posto al termine dell’articolo vi sono tre coppie di numeri primi gemelli). Non si è (ancora) stabilito come individuare teoricamente tali coppie e se esse sono infinite. Da parte mia osservo che il numero pari che separa la coppia è multiplo di sei. Questa proprietà è in parte simile a quella attribuita a Leibniz secondo cui, dato un qualsiasi numero primo, è multiplo di sei o il numero che lo precede o quello che lo segue.

1 - I numeri primi sono infiniti.

La dimostrazione di questa essenziale proprietà che è alla base di tutte le ricerche successive su tali numeri, risale ad Euclide (Elementi IX,20) e viene considerata una delle più belle dimostrazioni dell’intera matematica sia per la proprietà in sé e sia per la semplicità della dimostrazione: se i numeri primi fossero in numero finito, si può dimostrare che ve n’è almeno un altro non appartenente ad essi.

Se i numeri primi fossero, ad esempio, soltanto i numeri a; b; c; d allora  il numero abcd+1 non divisibile per alcuno di essi essendovi sempre il resto !, o è lui stesso un numero primo oppure è divisibile per un numero primo diverso da quelli supposti. In ogni caso dunque vi è un numero primo diverso da quelli supposti unici.

Notiamo che Eulero per altra strada ugualmente geniale dimostrerà l’infinità dei numeri primi. Tale dimostrazione verrà indicata nel paragrafo 3₆ di questa presentazione.

Vedremo inoltre nel teorema di Dirichlet un'altra connessione con l’infinità dei numeri primi.

2 - È possibile determinare intervalli numerici grandi a piacere privi di numeri primi.

Si supponga, ad esempio, che si voglia stabilire un intervallo di 50 numeri privo di numeri primi (lo stessa procedura si potrebbe seguire se l’intervallo si volesse di cento o cento miliardi di numeri e così via).

Si consideri il numero “fattoriale”:

(51)! = 1·2·3·4·…·50·51

Questo numero (di 65 cifre!) è quindi multiplo di 2; di 3: di 4 …di 51 e quindi sommandogli i numeri 2; 3; 4;  sino a 51 si otterrebbero numeri multipli di 2; di 3; di 4 …. di 51. In definitiva si otterrebbero 50 numeri non primi.

3 - Varie ipotesi sulla distribuzione dei numeri primi

3₁ -  Il Crivello di ERATOSTENE (276/272)- 195/192 a. C.)

La distribuzione dei numeri primi secondo il “Crivello” di ERATOSTENE consiste nello scrivere tutti i numeri naturali sino al numero minore del quale si vogliono determinare tutti i numeri primi.

Nella tabella che segue si è evidenziato il primo numero primo (l’unità non viene per opportunità considerato numero primo) e cioè il 2, si sono via via cancellati tutti i multipli di due (4; 6; 8 …).

 

 

 

Il secondo numero non cancellato è così il 3 (secondo numero primo) e si cancellano pertanto tutti multipli di 3 alcuni dei quali gà cancellati perché multipli anche di 2. Il numero seguente non cancellato è il 5 e si cancellano ora tutti i multipli di 5 cosicché operando in questo modo a partire ogni volta dal numero (primo) non cancellato rimangono nella tabella costituita da 1 a 100 i soli 25 numeri primi, minori di 100, non cancellati.

Come si vede  tra i numeri primi minori di cento vi sono otto coppie gemelle nelle quali il numero intermedio, come abbiamo già osservato è multiplo di sei. Così abbiamo già detto che risale a Leibniz l’osservazione secondo la quale, con p numero primo, uno dei due numeri p-1 oppure p+1 è multiplo di 6.  

A proposito della distribuzione dei numeri primi ricordiamo un risultato ottenuto nel  1954 da Gaetano Roberto Badalamenti che, mediante un regolo da lui intitolato (“Regolo della divisibilità” ma anche “Scompost”), consente di determinare rapidamente se un numero è o no primo e, nel caso non lo fosse, stabilire i fattori componenti [1_b].

3₂ -   Formula di FERMAT (1601-1665)

Fermat aveva creduto che la formula da lui pensata

potesse dare sempre numeri primi al variare di n. Questo è vero ad esempio per n = 0 ottenendo infatti 3; per n=1 ottenendo 5; per n=2 ottenendo 17 e così per n = 3 e  n=4. Ma Eulero mostrò che per n=5 si otteneva il numero 4.294.967 297 non primo poiché risultava uguale al prodotto  6 700 417 x 641.

3₃ -    Congettura di Goldbach (1690-1764)

La congettura, esposta in modo più semplice da Eulero a cui Goldbach si era rivolto, afferma che un qualsiasi numero pari è uguale alla somma di almeno una coppia di numeri primi anche se uguali.

Ad esempio

12 = 5 + 7

18 = 5 + 13   (ma anche a 7 + 11);

26 = 13 + 13   (ma anche a 7 + 19)

La dimostrazione di questa congettura ha impegnato tutti i matematici esperti o non esperti in teoria dei numeri ed è stata verificata per un numero incredibile di numeri sino a 400 000 000 000 000 notizia che è riportata nel  nel volume [1] L’Enigma dei Numeri Primi, p.61.

Osserviamo che poiché i numeri primi sono infiniti lo sono anche le loro coppie e quindi  i numeri pari dati dalle loro somme ma infiniti non vuol dire tutti e non fornisce in questo caso nessuna indicazione utile per la dimostrazione della congettura.

Sarebbe assai lungo e ci sarebbe bisogno di molta matematica per riportare tutti i tentativi volti alla dimostrazione della congettura di Goldbach che talvolta hanno comunque prodotto risultati e proprietà di teoria dei numeri. A questo proposito riportiamo una notevole affermazione di Hilbert che prendiamo dal libro Zio Petrose e la Cogettura di Goldbach ([2] pp. 39-40). Alla domanda fatta ad Hilbert sul perché non si fosse applicato alla risoluzione della congettura di Riemann (congettura sempre relativa ai numeri primi e che vedremo nel seguito), egli rispose che risolvere una congettura importante sarebbe stato come uccidere una gallina dalle uova d’oro intendendo con questo che risolvere tale congettura (o altre evidentemente) avrebbe impedito a tanti matematici di ottenere risultati importanti anche se non conclusivi per la congettura.

Tra i tanti risultati ottenuti nel tentativo di risolvere la nostra congettura ricordiamo una proprietà di una notevole  bellezza (scusate l’enfasi): Se la congettura di Goldbach si suppone vera allora si può dimostrare che un qualsiasi numero naturale maggiore di 3 è sempre equidistante tra due numeri primi::

Ad esempio  10 è equidistante tra 7 e 13:   23 è equidistante tra 17 e 29,

La dimostrazione è assai rapida poiché dato un qualsiasi numero n (>3) il suo doppio 2n è uguale, per la congettura, alla somma di due numeri primi p e q, cioè 2n = p + q da cui la formula del loro punto medio 

La proprietà può essere invertita: se ogni numero n è equidistante da due numeri primi e cioè  (p + q)/2 = n  allora il numero pari 2n  è la somma di questi e si giunge così alla congettura di Goldbach. In altre parole le due proprietà sono equivalenti.

Così, ammessa la congettura di Goldbach, si ottiene che un qualunque numero dispari maggiore di cinque è sempre uguale alla somma di tre numeri primi. Infatti, considerato un numero dispari, si tolga ad esso un numero primo e si sostituisca al resto (pari) la somma di due numeri primi secondo la congettura.

Esempio:  il numero dispari dato sia 35 e gli si tolga il numero primo 3 ottenendo 35 = 3 + 32 e si sostituisca a 32 la somma di due numeri primi  che esistono secondo la congettura supposta vera, ad esempio  32 = 13 + 19  (ma anche 3+29)

Si ha dunque:  35 = 3 + 13 + 19  (ma anche 35 = 3+3+29)

Si noti che  invertendo la relazione e cioè supponendo che un qualunque numero dispari (>5) si possa sempre ottenere come somma di tre numeri primi portando uno di questi al primo membro si ottiene un numero pari uguale alla somma di due numeri primi.

3₄ -  Formula di Eulero (1707-1783)

Abbiamo visto che Eulero aveva mostrato non vera la formula che Fermat considerava generatrice di numeri primi; da parte sua egli stabilisce una formula capace di generare numeri primi per n = 1, 2, 3, …40 :

n² – n + 41

Naturalmente Eulero non poteva ignorare che per n = 41, ottenendo dalla formula 41², non si aveva più un numero primo. Personalmente, per curiosità, ho calcolato la formula per i quarantadue numeri:  n =  42; 43; …83  trovando solo sette numeri non primi (n = 45; 50; 57; 66; 77; 82; 83).

Dal volume Numeri di Bruno D’Amore e Paolo Oliva ([3], p. 153) ho tratto una formula analoga n² – 79n +1601 dalla quale si determinano numeri primi per n < 80. Lascio al lettore la verifica di questa affermazione che ho controllato solo per n = 0; 1, 2, 3.

Riguardo ad Eulero vedremo, come già detto, nel paragrafo 3₆ la sua dimostrazione dell’infinità dei numeri primi.

3₅ -     Un teorema di John Wilson (1741-1793)

Il teorema di Wilson sui numeri primi, così viene indicato, sembra fosse già noto al matematico persiano Alhazen  intorno all'anno mille.

Se un numero n  è tale che  2x3x4x….x (n-1) + 1  è  multiplo di n,  cioè

2x3x4x….x (n-1) + 1  = kn  allora n è primo..

Se n fosse infatti divisibile per 2, cioè n = 2n’, allora si avrebbe

2kn’ = 2x3x4x….x (n-1) + 1  ;  cioè

2 [kn^'- 3x4x….x (n-1)]=1

ma essendo la parentesi quadrata un numero intero l’uguaglianza non è possibile. Analogamente se si supponesse che n fosse multiplo di 3, oppure di 4 … di n-1  e questo mostra  che  n è primo.

Si noto che il teorema inverso (se un numero n è primo allora 2x3x4x….x (n-1) + 1  è multiplo di n) è stato poi dimostrato da Lagrange.

3₆ -    Un teorema di Lagrange (1736-1816)

Di Joseph-Louis Lagrange riportiamo il suo teorema sulla divisibilità di un numero primo.

Fissato un qualsiasi numero primo p maggiore di 2, la somma di tutti i numeri naturali minori di p è multiplo di p ed è multiplo di p anche la somma di tutti i prodotti a due a due di essi (prodotto di classe due) ed anche i prodotti di classe tre, quattro sino alla classe  p-2. Nel caso  dell’unica combinazione di classe  p-1, cioè 1x2x3x…x (p-1) per avere il multiplo di p si deve aggiungere l’unità secondo il teorema di Wilson.

Esempio. Sia  p=7 per cui 1+2+3+4+5+6 = 21 multiplo di 7.

Il prodotto di classe due è:

1(2+3+4+5+6) + 2(3+4+5+6) + 3(4+5+6) + 4(5+6) + 5(6) = 675 multiplo di 7.

Il prodotto di classe tre è:

1(2x3)+1(2x4)+1(2x5)+1(2x6)+1(3x4)+1(3x5)+1(3x6)+1 (4x5)+1(4x6)+1(5x6) +

2(3x4)+2(3x5)+2(3x6)+2(4x5)+2(4x6)+2(5x6)+3(4x5)+3(4x6)+3(5x6)+4(5x6)=735  multiplo di 7.

Il prodotto di classe quattro è:

1(2x3x4)+1(2x3x5)+1(2x3x6)+1(2x4x5)+1(2x4x6)+1(2x5x6)+1(3x4x5)+1(3x4x6)+1(3x5x6)++1(4x5x6)+2(3x4x5)+2(3x4x6)+2(3x5x6)+2(4x5x6)+3(4x5x6)=1624  multiplo di 7

Il prodotto di classe 5 è:

1(2x3x4x5)+1(2x3x4x6)+1(2x3x5x6)+1(2x4x5x6x)+1(3x4x5x6)+2(3x4x5x6)=1764  multiplo di 7.

Ed infine consideriamo l’unico prodotto di classe 6 che con l’aggiunta di 1 diventa multiplo di 7 secondo il teorema di Wilson riportato nel paragrafo precedente: 1x2x3x4x5x6 + 1 = 721.

3₇ -  Peter Gustav Dirichlet (1805-1859) e Eulero (1707-1783) sull’infinità dei numeri primi

In questo paragrafo 3, nella rassegna di alcuni teoremi o alcune congettura relative all’infinità dei numeri primi, ricordiamo il teorema di Dirichlet secondo il quale la progressione  a_n = rn + s  contiene infiniti numeri primi se “r” ed “s” sono numeri tra loro primi.

Per arrivare alla dimostrazione di Eulero sulla infinità dei numeri primi si deve osservare lo studio e lo sviluppo della  cosiddetta “serie armonica”:

 

In vari modi si può dimostrare che tale serie diverge. Teniamo però presente che i denominatori sono i numeri interi. Vi s arà ad esempio il numero 120 ma tale numero scomposto nei vari numeri primi che lo compongono si può scriver come  2³ x 3 x5  e la frazione 1/120  come 1/2³1/3 1/5     . Pensando di operare in questo modo con tutte le frazioni della serie e raccogliendo successivamente i numeri primi uguali tra loro anche se con esponenti diversi, si ha:

 

Ebbene, se i numeri primi fossero finiti le parentesi sarebbero in numero limitato e il loro prodotto non potrebbe essere infinito come invece è il primo membro. I numeri primi sono quindi infiniti.

Ill secondo membro si può sintetizzare prima scrivendo il prodotto degli infiniti addendi e poi applicando la somma egli infiniti i termini di una progressione geometrica^[2]

 

Notiamo infine che Eulero estese tale serie a quella che chiamò “funzione zeta”. e che indicò con Ȥ(x) Questa funzione verrà poi impropriamente chiamata “funzione zeta di Riemann” per l’uso notevole che di essa ne fece.

 

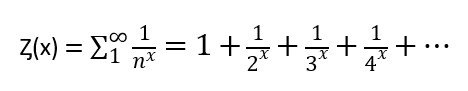
4  Carl Friedrich Gauss (1777-1855)

Nel paragrafo precedente abbiamo visto vari tentativi di esprimere infiniti numeri primi ma senza ottenere risultati significativi. Mutando tale prospettiva ed esaminando una particolare distribuzione dei nostri numeri primi, Gauss compì il primo approccio significativo in tal senso, il primo risultato su una distribuzione dei numeri primi che appariva senza alcuna legge.

Gauss osservò infatti, dato un numero qualsiasi n, ed indicando con π(n) la numerosità dei numeri primi minori di n una qualche relazione. Nella figura che segue la prima colonna è costituita dai numeri n, la seconda dei corrispondenti π (n) e la terza il risultato di n/ π (n). Come si vede moltiplicando per 10 i vari numeri n a partire da 10, il rapporto n/ π (n) cresce  di circa 2.

 

Senza percorrere i vari tentativi di Gauss, si può comunque notare una certa regolarità che aumenterà allorché egli si servì della funzione logaritmica in grado di porre un legame tra moltiplicazioni e addizioni, ottenendo in tal modo la prima grande ipotesi sulla distribuzione dei numeri primi:

Si noti che il logaritmo  è il logaritmo naturale (di base e=2,71828…) e che l’approssimazione indicata da Gauss è sempre più prossima al crescere di n. (la congettura di Gauss verrà in seguito dimostrata indipendentemente da Jacques Hadamard e da J. de la Vallèe Poussin mantenendo sempre l’approssimazione indicata da Gauss).

Osserviamo che il risultato di Gauss è stato giudicato, un po’ enfaticamente a mio parere, come ”una delle scoperte più notevoli di tutta la matematica” (cfr. Che cos’è la matematica? di R. Courant e H. Robbins, ([4] p. 71)

5 Bernhard Riemann (1887-1920)

Con Riemann il grande risultato di Gauss si sviluppa ulteriormente combinandosi con la funzione zeta di Eulero [ Ȥ(x) ].

che si chiamerà impropriamente, come abbiamo già osservato “funzione zeta di Riemann”.

Riemann sostituisce alla variabile x la variabile complessa  z ^([3]) e riesce a stabilire, con l’espressione in numeri primi che abbiamo visto appunto con Eulero, che la funzione è tale che i suoi zeri risultano collegati ai numeri primi minori del numero n e che in questo caso la parte reale del numero complesso è uguale ad ½ .

 Un ordine verificato al solito per milioni di casi come è affermato da Enrique Graciàn nel suo libro (I Numeri Primi. Un cammino verso l’infinito, ([5], p. 106) non sufficienti per la dimostrazione per la quale non è sufficiente neppure una infinità di casi ma è necessario il “tutti”.

Questo collegamento straordinario dovrebbe comunque avere una spiegazione tale da indicare una qualche struttura ordinata dei numeri primi e portare ad una conoscenza inseguita da sempre. Oltre alla fama immortale che premierebbe l’eventuale solutore, egli guadagnerebbe anche un milione di dollari posti come premio

Notiamo che nella stessa pagina del libro citato poco sopra viene riportato un aneddoto relativo ad Hilbert cioè al grande matematico che nel Congresso Internazionale dei Matematici del 1900 aveva indicato 23 problemi che i matematici avrebbero dovuto risolvere nel secolo entrante (il problema di Riemann era l’ottavo). Riportiamo le parole del libro: «Una volta chiesero all’eminente matematico tedesco David Hilbert quale sarebbe stata la prima domanda che avrebbe posto ad un ipotetico congresso di matematici che si fosse celebrato cento anni dopo la sua morte e la sua risposta fu “Domanderei se la congettura di Riemann è stata dimostrata”»

Notiamo infine che molti teoremi sono stati dimostrati sulla base della congettura di Riemann, una base però non del tutto solida ma che, poeticamente possiamo dire, viene considerata assolutamente vera.

 

6  Il mistero dei numeri primi

Il mistero dei numeri primi di cui parleremo in quest’ultimo paragrafo potrebbe distruggere tutto quello che è stato detto sino ad ora. Per questo lo abbiamo messo alla fine del nostro lavoro per non rendere inutile tutto quello che è stato detto ma che comunque resta valido dal punto di vista storico e che inoltre ha consentito il conseguimento di molti risultati che altrimenti non sarebbero  stati ottenuti.

La circostanza che ora raccontiamo e che viene stranamente trascurata da molti studiosi che si sono applicati e si applicano tuttora ai numeri primi, nasce quando  il neurologo Oliver Sacks  osserva che due suoi pazienti, i giovani gemelli autistici, John e Michael, si scambiavano a voce alcuni numeri. Cosa strana poiché i due giovani erano assolutamente ignoranti in aritmetica non sapendo neppure fare le più semplici operazioni quali l’addizione e la sottrazione.

Fortunatamente Sacks era interessato ai numeri; ricordiamo ad esempio che sulla copertina del libro [2] ma penso anche sull’edizione originaria, egli presenta il libro che tratta della congettura di Goldbach: «Una congettura matematica–scrive tra l’altro- irrisolta».

Sacks, che ricorda l’episodio (cap. XXIII di [11]) narra che, incuriosito, trascrive i numeri che i due gemelli si scambiano sorridendo, numeri di sei cifre (ivi p. 263) che risultarono essere numeri primi. Sacks si munisce di una serie di numeri primi e  unendosi ai due fratelli enuncia un numero primo di otto cifre che viene riconosciuto dopo una certa esitazione dai due che accolgono il dottore nel loro gioco e i numeri primi diventano di nove e dieci cifre e persino di dodici cifre ma il neurologo non può più controllare né proseguire poiché il libro che egli consultava di nascosto, non andava su tali cifre. Con qualche intervallo di tempo maggiore di quello sino ad allora necessario per la riconoscenza di numeri primi, i due fratelli continuarono aumentando via via il numero delle cifre.

Ma come era stato possibile tutto ciò? Si potrebbe pensare, data la memoria straordinaria manifestata in altre circostanze dai due gemelli, che  si fossero imparate a memoria  la successione dei numeri primi? Questo sembra praticamente impossibile anche perché John e Michael, non avevano a disposizione alcun manuale, ammesso che ce ne esistesse uno così spinto. Ricordiamo inoltre che in una circostanza capitata sempre alla presenza di Sacks, caddero su il pavimento un insieme di fiammiferi e i due gemelli dissero immediatamente e contemporaneamente il numero (esatto!) degli oggetti: 111 e alla domanda di come avessero fatto risposero che l’avevano semplicemente letto!

Ma quale ordine può esserci tra i numeri primi che consentisse ai due gemelli di proseguire nel loro “gioco”, quell’ordine che invano i migliori matematici di ogni epoca hanno invano cercato di individuare? E in che modo il cervello poteva gestirlo? Sono domande assolutamente sconvolgenti.

Nel volume di Du Sautoy ([1] p.21) viene riportato lo stupore di un grande matematico, specializzato in teoria dei numeri, Enrico Bombieri (Milano 1940):

«Per me è difficile ascoltare questa storia senza sentirmi intimidito e strabiliato di fronte al funzionamento del cervello. Ma mi chiedo: i miei amici non matematici hanno la stessa reazione? Hanno la più vaga idea di quanto fosse bizzarro, prodigioso e perfino ultraterreno il singolare talento che i due gemelli possedevano in modo naturale? Sono consci del fatto che da secoli i matematici si sforzano di trovare una maniera per fare quello che John e Michael facevano spontaneamente: generare e riconoscere dei numeri primi?»

Riusciremo mai a capire quello che ancora oggi è il mistero dei numeri primi, uno degli argomenti matematici più belli e insidiosi di tutta la matematica? Euclide ha indicato la loro infinità, Gauss ne ha mostrato un certo ordine, Riemann ha sfiorato una loro proprietà ma i due gemelli, separati per dar loro una qualche possibilità individuale di inserimento nel mondo e così vanificando il tesoro che si celava in essi, hanno mostrato l’esistenza incredibile di uno dei problemi più affascinanti della matematica e del cervello umano.

 

BIBLIOGRAFIA

[1] Marcus De Sautoy L’Enigma dei Numeri Primi. L’ipotesi di Riemann il più grande mistero dell’Umanita’, Rizzoli,  VI ed.2004, pp. 608

[1_a] George Gheverghese Joseph, C’era una volta l numero. La vera storia della matematica, Saggiatore, Milano, 2003, pp. 444

[1_b] Gaetano Roberto Badalamenti, A spasso fra numeri e numeri primi. Si sgretola il mistero dei numeri primi., Ed. Beta, Roma 1996, pp.32

[2] Apostolos Doxiadis, Zio Petros e la congettua di Goldbach, Bompiani, 2000, pp. 143

[3] Bruno D’Amore, Paolo Oliva, Numeri, FrancoAngeli, Milano, 1994, pp.334

[4] Richard Courant, Herbert Robbins, Che cos’è la Matematica? Einaudi, 1950, pp.752

[5] Enriques Graciàn, I numeri primi. Un lungo cammino verso l’infinito. Mondo Matematico, Milano, 2012, pp. 143

[6] Cogliati Alberto, Riemann. La geometria dello spazio curvo, Ed. Corriere della Sera, Milano 2016, pp. 152

[7] Gauss. Una rivoluzione nella teoria dei numeri   

[8] Matematica, Ed. ed. Garzantini, 2013, pp. 1515

[9] Rufiàn Lizana Antonio, Gauss.Una rivoluzione nella teoria dei numeri, RBA Italia, 2012, pp. 167

[10] Scarpis Umberto, Sui numeri primi e sui problemi dell’analisi indeterminata, in Questioni riguardanti le matematiche elementari, , Parte seconda e terza, Zanichelli, 1983, pp. 1-98  

[11] O=livier Sacks, L’uomo che scambiò una moglie per un cappello, Adelphi, XI ed.  2008. pp. 318

 

Tabella dei numeri primi fino a 10.957

 

---	2	3	5	7	11	13	17	19	23	29	31
37	41	43	47	53	59	61	67	71	73	79	83
89	97	101	103	107	109	113	127	131	137	139	149
151	157	163	167	173	179	181	191	193	197	199	211
223	227	229	233	239	241	251	257	263	269	271	277
281	283	293	307	311	313	317	331	337	347	349	353
359	367	373	379	383	389	397	401	409	419	421	431
433	439	443	449	457	461	463	467	479	487	491	499
503	509	521	523	541	547	557	563	569	571	577	587
593	599	601	607	613	617	619	631	641	643	647	653
659	661	673	677	683	691	701	709	719	727	733	739
743	751	757	761	769	773	787	797	809	811	821	823
827	829	839	853	857	859	863	877	881	883	887	907
911	919	929	937	941	947	953	967	971	977	983	991
997	1009	1013	1019	1021	1031	1033	1039	1049	1051	1061	1063
1069	1087	1091	1093	1097	1103	1109	1117	1123	1129	1151	1153
1163	1171	1181	1187	1193	1201	1213	1217	1223	1229	1231	1237
1249	1259	1277	1279	1283	1289	1291	1297	1301	1303	1307	1319
1321	1327	1361	1367	1373	1381	1399	1409	1423	1427	1429	1433
1439	1447	1451	1453	1459	1471	1481	1483	1487	1489	1493	1499
1511	1523	1531	1543	1549	1553	1559	1567	1571	1579	1583	1597
1601	1607	1609	1613	1619	1621	1627	1637	1657	1663	1667	1669
1693	1697	1699	1709	1721	1723	1733	1741	1747	1753	1759	1777
1783	1787	1789	1801	1811	1823	1831	1847	1861	1867	1871	1873
1877	1879	1889	1901	1907	1913	1931	1933	1949	1951	1973	1979
1987	1993	1997	1999	2003	2011	2017	2027	2029	2039	2053	2063
2069	2081	2083	2087	2089	2099	2111	2113	2129	2131	2137	2141
2143	2153	2161	2179	2203	2207	2213	2221	2237	2239	2243	2251
2267	2269	2273	2281	2287	2293	2297	2309	2311	2333	2339	2341
2347	2351	2357	2371	2377	2381	2383	2389	2393	2399	2411	2417
2423	2437	2441	2447	2459	2467	2473	2477	2503	2521	2531	2539
2543	2549	2551	2557	2579	2591	2593	2609	2617	2621	2633	2647
2657	2659	2663	2671	2677	2683	2687	2689	2693	2699	2707	2711
2713	2719	2729	2731	2741	2749	2753	2767	2777	2789	2791	2797
2801	2803	2819	2833	2837	2843	2851	2857	2861	2879	2887	2897
2903	2909	2917	2927	2939	2953	2957	2963	2969	2971	2999	3001
3011	3019	3023	3037	3041	3049	3061	3067	3079	3083	3089	3109
3119	3121	3137	3163	3167	3169	3181	3187	3191	3203	3209	3217
3221	3229	3251	3253	3257	3259	3271	3299	3301	3307	3313	3319
3323	3329	3331	3343	3347	3359	3361	3371	3373	3389	3391	3407
3413	3433	3449	3457	3461	3463	3467	3469	3491	3499	3511	3517
3527	3529	3533	3539	3541	3547	3557	3559	3571	3581	3583	3593
3607	3613	3617	3623	3631	3637	3643	3659	3671	3673	3677	3691
3697	3701	3709	3719	3727	3733	3739	3761	3767	3769	3779	3793
3797	3803	3821	3823	3833	3847	3851	3853	3863	3877	3881	3889
3907	3911	3917	3919	3923	3929	3931	3943	3947	3967	3989	4001
4003	4007	4013	4019	4021	4027	4049	4051	4057	4073	4079	4091
4093	4099	4111	4127	4129	4133	4139	4153	4157	4159	4177	4201
4211	4217	4219	4229	4231	4241	4243	4253	4259	4261	4271	4273
4283	4289	4297	4327	4337	4339	4349	4357	4363	4373	4391	4397
4409	4421	4423	4441	4447	4451	4457	4463	4481	4483	4493	4507
4513	4517	4519	4523	4547	4549	4561	4567	4583	4591	4597	4603
4621	4637	4639	4643	4649	4651	4657	4663	4673	4679	4691	4703
4721	4723	4729	4733	4751	4759	4783	4787	4789	4793	4799	4801
4813	4817	4831	4861	4871	4877	4889	4903	4909	4919	4931	4933
4937	4943	4951	4957	4967	4969	4973	4987	4993	4999	5003	5009
5011	5021	5023	5039	5051	5059	5077	5081	5087	5099	5101	5107
5113	5119	5147	5153	5167	5171	5179	5189	5197	5209	5227	5231
5233	5237	5261	5273	5279	5281	5297	5303	5309	5323	5333	5347
5351	5381	5387	5393	5399	5407	5413	5417	5419	5431	5437	5441
5443	5449	5471	5477	5479	5483	5501	5503	5507	5519	5521	5527
5531	5557	5563	5569	5573	5581	5591	5623	5639	5641	5647	5651
5653	5657	5659	5669	5683	5689	5693	5701	5711	5717	5737	5741
5743	5749	5779	5783	5791	5801	5807	5813	5821	5827	5839	5843
5849	5851	5857	5861	5867	5869	5879	5881	5897	5903	5923	5927
5939	5953	5981	5987	6007	6011	6029	6037	6043	6047	6053	6067
6073	6079	6089	6091	6101	6113	6121	6131	6133	6143	6151	6163
6173	6197	6199	6203	6211	6217	6221	6229	6247	6257	6263	6269
6271	6277	6287	6299	6301	6311	6317	6323	6329	6337	6343	6353
6359	6361	6367	6373	6379	6389	6397	6421	6427	6449	6451	6469
6473	6481	6491	6521	6529	6547	6551	6553	6563	6569	6571	6577
6581	6599	6607	6619	6637	6653	6659	6661	6673	6679	6689	6691
6701	6703	6709	6719	6733	6737	6761	6763	6779	6781	6791	6793
6803	6823	6827	6829	6833	6841	6857	6863	6869	6871	6883	6899
6907	6911	6917	6947	6949	6959	6961	6967	6971	6977	6983	6991
6997	7001	7013	7019	7027	7039	7043	7057	7069	7079	7103	7109
7121	7127	7129	7151	7159	7177	7187	7193	7207	7211	7213	7219
7229	7237	7243	7247	7253	7283	7297	7307	7309	7321	7331	7333
7349	7351	7369	7393	7411	7417	7433	7451	7457	7459	7477	7481
7487	7489	7499	7507	7517	7523	7529	7537	7541	7547	7549	7559
7561	7573	7577	7583	7589	7591	7603	7607	7621	7639	7643	7649
7669	7673	7681	7687	7691	7699	7703	7717	7723	7727	7741	7753
7757	7759	7789	7793	7817	7823	7829	7841	7853	7867	7873	7877
7879	7883	7901	7907	7919	7927	7933	7937	7949	7951	7963	7993
8009	8011	8017	8039	8053	8059	8069	8081	8087	8089	8093	8101
8111	8117	8123	8147	8161	8167	8171	8179	8191	8209	8219	8221
8231	8233	8237	8243	8263	8269	8273	8287	8291	8293	8297	8311
8317	8329	8353	8363	8369	8377	8387	8389	8419	8423	8429	8431
8443	8447	8461	8467	8501	8513	8521	8527	8537	8539	8543	8563
8573	8581	8597	8599	8609	8623	8627	8629	8641	8647	8663	8669
8677	8681	8689	8693	8699	8707	8713	8719	8731	8737	8741	8747
8753	8761	8779	8783	8803	8807	8819	8821	8831	8837	8839	8849
8861	8863	8867	8887	8893	8923	8929	8933	8941	8951	8963	8969
8971	8999	9001	9007	9011	9013	9029	9041	9043	9049	9059	9067
9091	9103	9109	9127	9133	9137	9151	9157	9161	9173	9181	9187
9199	9203	9209	9221	9227	9239	9241	9257	9277	9281	9283	9293
9311	9319	9323	9337	9341	9343	9349	9371	9377	9391	9397	9403
9413	9419	9421	9431	9433	9437	9439	9461	9463	9467	9473	9479
9491	9497	9511	9521	9533	9539	9547	9551	9587	9601	9613	9619
9623	9629	9631	9643	9649	9661	9677	9679	9689	9697	9719	9721
9733	9739	9743	9749	9767	9769	9781	9787	9791	9803	9811	9817
9829	9833	9839	9851	9857	9859	9871	9883	9887	9901	9907	9923
9929	9931	9941	9949	9967	9973	10007	10009	10037	10039	10061	10067
10069	10079	10091	10093	10099	10103	10111	10133	10139	10141	10151	10159
10163	10169	10177	10181	10193	10211	10223	10243	10247	10253	10259	10267
10271	10273	10289	10301	10303	10313	10321	10331	10333	10337	10343	10357
10369	10391	10399	10427	10429	10433	10453	10457	10459	10463	10477	10487
10499	10501	10513	10529	10531	10559	10567	10589	10597	10601	10607	10613
10627	10631	10639	10651	10657	10663	10667	10687	10691	10709	10711	10723
10729	10733	10739	10753	10771	10781	10789	10799	10831	10837	10847	10853
10859	10861	10867	10883	10889	10891	10903	10909	10937	10939	10949	10957

 

 

Un’applicazione dei numeri primi

Un altro problema affascinante, legato ai numeri primi, è quello relativo al “numero perfetto” cioè, secondo la definizione di Euclide (VII, def. 28): “Numero perfetto è quello che è uguale alla somma delle proprie parti”  intendendo con “parti” i divisori propri del numero.

Tutti i testi che parlano dei numer4i perfetti  indicano come primo esempio il numero 6 che infatti è uguale ai suoi divisori (propri): 1; 2; 3 e, di seguito il numero 28 uguale ai suoi divisori (propri) 1; 2; 4; 7: 14..

Fu Euclide a dimostrare (IX,36) la condizione sufficiente affinché un numero pari possa essere perfetto, dimostrazione che, in assenza di un simbolismo adeguato risulta di due fitte pagine nell’edizione curata da Attilio Frajese (UTET, 1970). Con il nostro simbolismo e sfruttando i “numeri di Marsenn” (2ⁿ – 1) la dimostrazione risulta semplificata.

C.S. perché il numero N pari espresso con il simbolo 2^n-1 (2ⁿ – 1) sia perfetto è che il numero di Marsenne (2ⁿ – 1) sia primo.

In tal caso, infatti i divisori (propri) del numero N  sono^[4]

1; 2; 2²; 2³;     2^n-1;   e   1(2ⁿ – 1); 2(2ⁿ – 1); 2²(2ⁿ – 1); 2³(2ⁿ – 1);    2^n-2(2ⁿ – 1)

 e la loro somma, (progressioni geometriche):

2ⁿ – 1   +    (2ⁿ – 1)(1 +  2 + 2² ₊ 2³  +   2^n-2)  = (2ⁿ – 1) [1 + (2^n-1 – 1)]  =  (2ⁿ – 1) 2^n-1 = N 

Più complicato, matematicamente, è la dimostrazione della condizione necessaria ad opera di Eulero, secondo la quale se un numero pari è perfetto non può essere che della forma 2^n-1 (2ⁿ – 1)  vista^[5].

Anche nel caso dei numeri perfetti vi sono delle domande alle quali ancora non vi è stata data ancora risposta: i numeri perfetti sono infiniti? Vi sono numeri perfetti dispari? Abbiamo però trattato i numeri perfetti solo per il loro legame con i numeri primi. Ricordiamo però la simpatica ma poco credibile teoria di Sant’Agostino secondo la quale Dio avrebbe voluto creare l’universo proprio in sei giorni perché numero perfetto (Agostino, La città di Dio, XI,39). E ricordiamo soltanto che con una semplice costatazione si potrebbe mostrare che i numeri perfetti (pari) devono terminare  o con  6 oppure con 8.

I primi 12 numeri perfetti sono:

• 6
• 28
• 496
• 8 128
• 33 550 336 (8 cifre)
• 8 589 869 056 (10 cifre)
• 137 438 691 328 (12 cifre)
• 2 305 843 008 139 952 128 (19 cifre)
• 2 658 455 991 569 831 744 654 692 615 953 842 176 (37 cifre)
• 191 561 942 608 236 107 294 793 378 084 303 638 130 997 321 548 169 216 (54 cifre)
• 13 164 036 458 569 648 337 239 753 460 458 722 910 223 472 318 386 943 117 783 728 128 (65 cifre)
• 14 474 011 154 664 524 427 946 373 126 085 988 481 573 677 491 474 835 889 066 354 349 131 199 152 128 (77 cifre)

Il successivo numero perfetto, il tredicesimo, è composto da 314 cifre. Fino ad ora (ottobre 2024)  si conoscono solo 52 numeri perfetti. Il più grande tra questi è 2^136279840 × (2^136279840 − 1), formato (in base 10) da 82048639 cifre^[6] .

^[4] Non si considera il divisore  2^n-1(2ⁿ – 1) poiché è il numero N dato e noi vogliamo si considerare    solo quelli propri

 

^[5] Una esposizione più completa dell’argomento dei numeri perfetti si può trovare, anche per vari riferimenti bibliografici, in un mio articolo stampato sulla rivista “Periodico di Matematiche” del 2012 (n.1; pp. 49-64).

^[6]  La tabella  e la conclusione finale sono state prese da Google.

 

^[3] Si noti che , detti “a”  e “b” due numeri reali, allora °a + ib”è un numero complesso  co  “i =

^[2] [1] Si ricordi che la somma  S_n di  n termini di una progressione geometrica  a + aq + aq²  + aq³ +   + aq^n-1 è S_n = a  e nel caso di infini termini con |q| < 1, S_n =

^[1]Si tenga presente che  I numeri interi posti tra parentesi quadrate indicano  i testi della biografia.