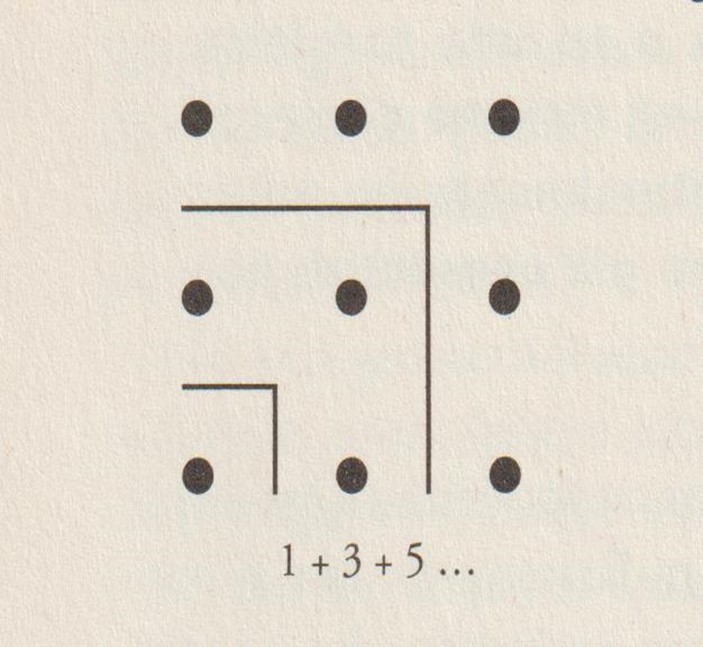Alcune considerazioni sui numeri interi

di Silvio Maracchia

 

Il numero intero è un elemento insostituibile in una società di qualunque livello tanto che Eschilo (525 circa – 456-455 a.C.), il grande drammaturgo greco, ne fa oggetto fondamentale per l’evoluzione dell’uomo e Platone (427-347 a. C.) il grande filosofo, afferma che togliere all’uomo il numero significherebbe togliergli la saggezza.

Eschilo, Prometeo (Secondo Episodio, v. 459, passim, nella traduzione di Ettore Romagnoli). Il dio Prometeo viene torturato da Giove poiché, aveva tratto l’uomo dallo stato selvaggio «…ogni loro opera/ senza discernimento era, sin che/ esperti li resi a consultar le stelle/e il sorger loro ed i tramonti arcani./E poi rinvenni, a lor vantaggio, il numero,/somma fra le scienze, e le compagini/ di lettere, ove la Memoria serbasi/ che Madre operatrice è delle Muse.»

Platone Epinomide 977c (ma anche in Repubblica 522c sgg. e in Leggi 818 c-d): «Se togliessimo il numero dalla natura umana non potremmo mai essere saggi. Mai difatti l’anima dell’essere vivente che mancasse di ragione potrebbe afferrare la virtù tutta quanta. Un essere che non sapesse conoscere il due e il tre, il dispari ed il pari ed ignorasse totalmente il numero non potrebbe mai rendere ragione di ciò di cui non avrebbe che sensazioni e ricordi»

Non solo Eschilo attribuisce la nascita del numero ad un regalo di una divinità, ma anche lo stesso Platone attribuisce al dio egiziano Theut la creazione del numero assieme all’astronomia, alla geometria e alla scrittura (Leggi 274 g) e in un altro luogo (Timeo 53 b) è sempre un dio (Demiurgo) che mette ordine al caos iniziale mediante “forme e numeri”.

Sarebbe lungo ricordare l’attribuzione divina alla nascita del numero e dell’ordinamento matematico che ne consegue, così, ad esempio, nella Bibbia (Sapienza 11,20); in Sant’Agostino (Città di Dio XI,30); in Galileo (Il Saggiatore, Examen Primum; p.147 nel vol. primo dell’ed. Salani del 1964) e in Keplero (Prefazione del Mysterium Cosmographicum) e anche recentemente con Benedetto XVI (Convegno di Verona, 2006).

Ma tutte queste considerazioni diventano quasi casi particolari della teoria pitagorica secondo la quale “tutto è numero”. A questo proposito leggiamo il brano di Aristotele uno dei più attendibili studiosi del pitagorismo su cui aveva scritto anche un lavoro andato smarrito (Metafisica 985 b 23 sgg.).

«Contemporaneamente a quei filosofi [Anassagora; Empedocle; Leucippo, Democrito] ed anche anteriori a questi, sono i cosiddetti pitagorici. Essi per primi si applicarono alle matematiche e le fecero progredire e, nutriti delle medesime, credettero che i principi di queste fossero principi di tutti gli esseri .E poiché nelle matematiche i numeri sono per loro natura i principi primi, e appunto nei numeri essi ritenevano di vedere più che nel fuoco e nella terra e nell’acqua molte somiglianze con le cose che sono e che si generano […] e, infine, poiché tutte le altre cose, in tutta la realtà, pareva a loro che fossero fatte a immagine dei numeri e che i numeri fossero ciò che è primo in tutta quanta la realtà, pensavano che gli elementi dei numeri fossero elementi di tutte le cose e che tutto quanto il cielo fosse armonia e numero». Si veda anche un altro passo della Metafisica (1090 a, 20 sgg.) ove Aristotele attribuisce ai Pitagorici la sensibilità dei numeri poiché presenti nelle cose sensibili e pertanto costituenti di esse.

 

RISULTATI DELLE CIVILTA’ PRE-ELLENICHE

Premessa: Ancora prima delle civiltà sumero, babilonese, egiziana una ipotesi attendibile (cfr. le prime righe di Fato antico di G, De Santillana, Adelphi, Milano, 1985) considera la prima creazione dei numeri o perlomeno la loro presenza, dalla contemplazione astronomica arcaica.

UN PRESTIGIOSO RISULTATO DALL’ARITMETICA BABILONESE

La numerazione babilonese^[1] segue talvolta anche un criterio posizionale di cui poniamo un semplice esempio

 

 

 

 

 

 

              1                       10                                                                    1*60 + 35/60

Nella tavoletta n. 322 della collezione “Plimpton” indicata solitamente con “Plimpton ” 322” (datata tra il 1800 e il 1600 a. C circa) sono indicate quindici terne di numeri da tutti gli storici considerate delle terne cosiddette “pitagoriche” e cioè delle ter ne tali che la somma dei quadrati di due di essi è uguale al quadrato del terzo, come accade tra i cateti e l’ipotenusa di un triangolo rettangolo ( b² + l² = d²) come ad esempio con i numeri 3, 4, e 5.

  

 

 

 

 

 

 

 

  

 

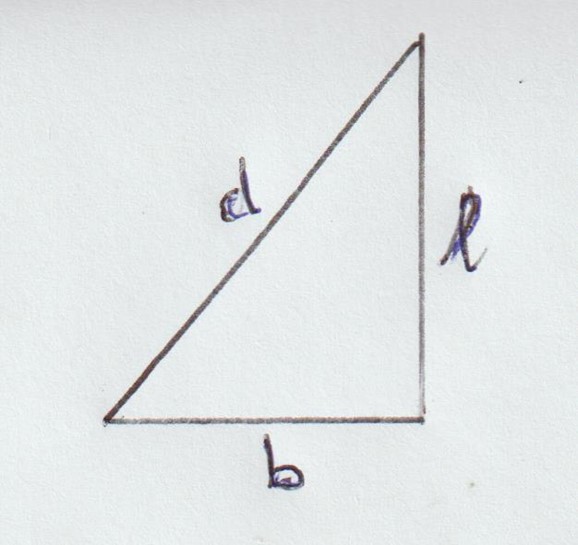
                                                                                                                                                                                                nella tavoletta sono indicati i valori di b, di d e del rapporto d²/l²

Sarebbe molto lungo riportare ed esaminare le varie ipotesi che sono state fatte sia per il conseguimento delle terne e sia sul perché di esse; ci limitiamo ad indicare la più piccola delle terne della Plimpton: 45, 60, 75 e la più grande: 12.709, 13.500, 18.541

Qualunque sia stato lo scopo di queste terne, esse mostrano il buon livello che era stato raggiunto dalla teoria dei numeri dei babilonesi (oltre che nella geometria e nell’algebra di cui non ci occupiamo in questa sede).

UN RISULTATO DALL’ARITMETICA EGIZIANA

La numerazione egiziana espressa con geroglifici

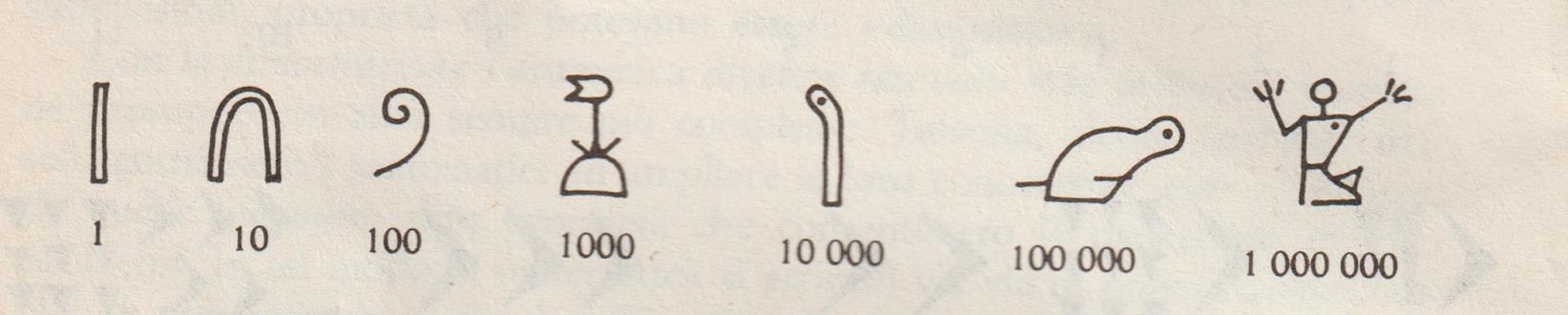
Anche la matematica egiziana raggiunse risultati notevoli sia nel campo della geometria, dell’aritmetica e dell’algebra. Noi, mostreremo un solo risultato tratto dal più grande tra i papiri matematici a noi pervenuti e cioè dal “papiro Rhind” (Rhind è il nome dell’acquirente del papiro, le dimensioni sono   5,64 metri per la lunghezza e 33,02 centimetri per la larghezza e consta di 85 problemi) risalente al 1600 a. C. circa ma, come copia eseguita dallo scriba Ahmes, risalente ad un periodo anteriore.

Ebbene nel problema n. 79 viene mostrata la moltiplicazione tra due numeri, eseguita scomponendo uno dei due nella somma delle potenze di due (compreso eventualmente 1) in modo da ottenere il risultato raddoppiando via via il secondo numero e prendendo solo quei doppi in corrispondenza alle potenze che avevano per somma il primo numero.

Ad esempio, volendo moltiplicare 13 per 42 (il problema n. 79 porta a numeri più grandi), poiché 13 = 1 + 4 + 8 si ha:

1*       2       4*       8*   …

42     84     168   336      basta allora sommare 42 + 168 + 336 per avere 546

Ma si potrebbe anche scomporre 42 che è 2 + 8 + 32, pertanto:

1       2*     4     8*       16       32*

13   26     52   104    208       416     e quindi: 26 + 104 + 416 = 546

In altre parole se prendiamo per esempio il primo caso, non si fa altro che operare nel metodo seguente:

13 x 42 = (1 + 4+ 8) x 42 = 42 + 168 + 336          

In realtà il problema 79 del papiro Rhind presenta il seguente problema: «In una proprietà vi sono sette case; in ogni casa vi sono sette gatti; ogni gatto acchiappa sette topi; ogni topo mangia sette spighe e in ogni spiga vi sono sette grani. Quante cose ci sono in tutta questa storia?»

Il probleam porta dunque al numero (trascurando la “proprietà”) al numero:

7 + 7² + 7³ + 7⁴ + 7⁵ che viene risolta nel papiro considerando il numero 2801 e successivamente 2801 + 5608 + 11204 = 19607.

In altre parole il matematico egiziano ha operato considerando prima una sola casa per cui le “cose” sono soltanto 1 + 7 + 7² + 7³ + 7⁴ = 2801 e successivamente considerando le sette case, ha moltiplicato ha moltiplicato per 7 con il metodo indicato sopra:

1*                     2*                 4*

2801               5608             11204

Sommando infine i valori trovati.

Quello che è significativo a cui non è stato data però importanza è la possibilità di poter scrivere qualsiasi numero tramite le potenze del 2 e con l’eventuale aggiunta dell’1 che noi possiamo intendere anche con 2⁰. Ebbene questo è appunto quello che secoli, anzi millenni, dopo, si è raggiunto mediante quel metodo che oggi va sotto il nome di “sistema binario” così importante per lo sviluppo dei circuiti in campo elettronico. In questo caso, volendo scrivere 13 con tale metodo si ha:

1011 (cioè 1+4+8) e il 42 con 010101 (cioè 2+8+32) intendendo i vari posti quali potenze del 2, cioè: 2⁰; 2¹; 2²; 2³ ecc. e indicando con lo zero l’assenza e con 1 la presenza di quella particolare potenza. Noi però oggi scriveremmo il numero secondo il nostro modo e cioè dalla potenza più grande alla più piccola e quindi per il 42, capovolgendo quanto scritto sopra, scriveremmo 1101 per il 13 e 101010 per 42.

ARITMETICA GRECA

I numeri sono indicati attraverso le lettere dell’alfabeto

 

A quanto risulta dalle analisi delle matematiche pre-elleniche, pur con risultati notevoli, non si erano suddivisi i numeri e non si erano cercate dimostrazioni delle proprietà comunque raggiunte o non si erano messe in evidenza.

I matematici greci e in modo particolare i matematici pitagorici, avevano subito cominciato a dividere i numeri a secondo alcune loro caratteristiche. Si ebbero quindi i numeri dispari e i numeri pari, i numeri quadrati e cubi, numeri poligonali di vario tipo, numeri primi, numeri perfetti e altre suddivisioni ormai non più considerati (n. eccedenti, deficienti, parimpari, parimente pari, eteromechi, ecc . di cui trascuriamo le definizioni).

Esaminiamo i numeri dispari e osserviamo alcune loro caratteristiche, note ai matematici greci e talvolta dimostrate, caratteristiche che in questa sede rimarranno solo indicate.

1 3 5 7 9 11 13 15 17 19 21   23   25   sino all’ennesimo… (2n-1)

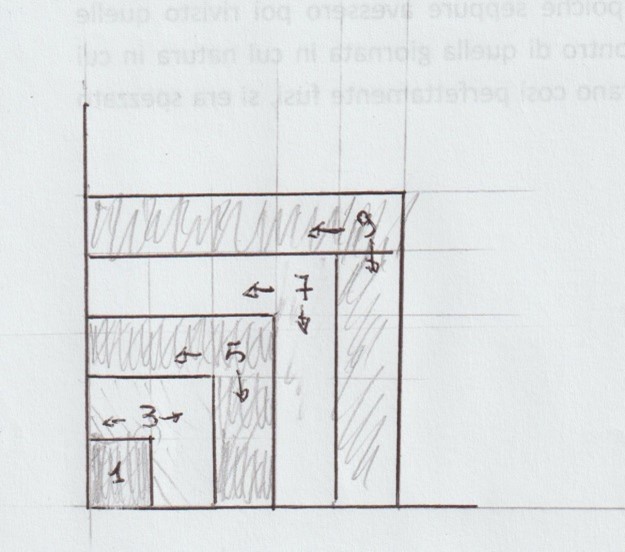
Se osserviamo, ad esempio, la somma dei primi due o tre o quattro o cinque e così via dei numeri dispari a partire dall’unità, possiamo constatare che tali somme sono rispettivamente uguali al quadrato di 2, di 3, di 4, di 5 e così via (ad esempio la somma dei primi quattro numeri dispari a partire dall’unità (1+3+5+7) è uguale a 16 cioè a quattro al quadrato. Così la somma dei primi n nume dispari, indicati sopra, è uguale a n²

Questa proprietà la di può osservare in quella parte della matematica coltivata dai pitagorici e successivamente da molti matematici greci e no e cioè nell’aritmo-geometria

 

Si osservi il quadratino su cui è stato scritto 1, se gli aggiungono i tre quadratini superiori su cui scritti 3, si ottiene come risultato un quadrato di 4 quadratini (1+3=4); se al quadrato ottenuto si aggiungono 5 quadratini indicati dal 5 si ottiene un quadrato totale di 9 quadratini (1+3+5=9) e così via. I Pitagorici usavano anche i “punti” (“psefoi” o anche “monadi”) per la loro aritmo-geometria

 

 

Consideriamo ora il primo numeri dispari (1), poi la somma dei due seguenti (3+5), poi ancora la somma dei tre seguenti (7+9+11) e così via. In questo caso si ottengono via via i numeri cubi a partire dall’unità e cioè, nell’esempio: 1³, 2³; 3³ ecc.    

Ebbene, combinando le due proprietà indicate si ottiene rapidamente una delle più belle formule dell’aritmetica, quella formula che lo storico, logico e matematico Giovanni Vailati non poteva vedere senza provare un senso di vertigine:

1³ + 2³ + 3³ + 4³ + … n³ = (1 + 2 + 3 + 4 + …n)²

La geometria legata all’aritmetica come abbiamo visto sopra, portò a voler affrontare vari quesiti di un ramo anche con l’altro. Ad esempio, dato un quadrato è semplice riuscire a costruirne un altro doppio ma quando si volle determinare aritmeticamente la misura del lato di questo secondo quadrato si vide che i numeri naturali non sarebbero stati sufficienti per risolvere il problema. Questo viene raccontato da Platone (Menone 82 a – 85 b) che probabilmente volle mostrare che fu proprio questa difficoltà che portò ad una conseguenza inaspettata: la nascita delle grandezze incommensurabili

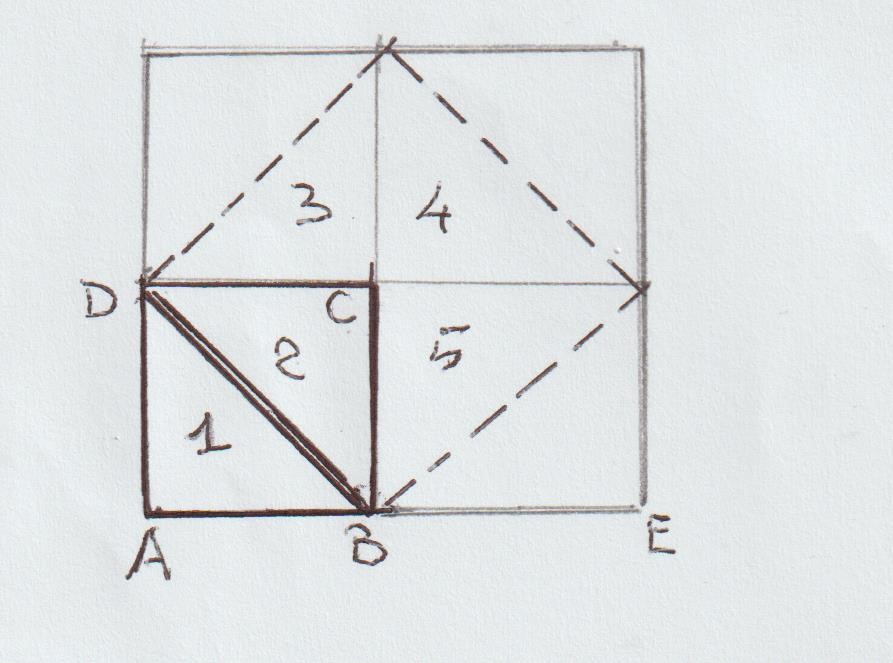
Dato il quadrato ABCD, il lato AB misuri 2, come afferma Platone; l’area è dunque 4. Si cerca il lato del quadrato che abbia area doppia ma con il lato doppio AE si ottiene un quadrato di area 16 e neppure con il lato di misura 3 (area 9). Il problema non si risolve neppure considerando una frazione che sia maggiore di 2 e minore di 3 ad esempio 2+ 1/n con n>1, poiché si ricadrebbe sempre nei numeri interi, per i quali risulterebbe sempre impossibile la soluzione, infatti considerando come unità di misura 1/n di quella di partenza AB misurerebbe il numero intero 2n + 1.

Eppure, afferma Socrate, il segmento richiesto è DB il cui quadrato è dato dai triangoli 2; 3; 4; 5 doppio del quadrato costituito dai soli triangoli (uguali ai precedenti) 1 e 2.

Ma allora il problema diventa: quanto sarà la misura di BD? Ebbene, a parte l’esempio numerico si tratta di stabilire se in un quadrato il lato e la sua diagonale possano avere una comune unità di misura.

Indichiamo con “a” la misura del lato AB e con “b” quella della diagonale BD supponendoli entrambi numeri interi e primi tra loro per la scelta della massima unità di misura. Il teorema di Pitagora applicato al triangolo rettangolo ABD porta pertanto alla relazione.

b² = 2a²  

ma questa relazione, con una dimostrazione che risulta essere una delle prime dimostrazioni della matematica, risulta impossibile poiché si giungerebbe all’assurdo che uno stesso numero dovrebbe essere sia pari che dispari (a questo proposito vi è un significativo accenno di Aristotele in Analitici Primi 41 a 23-30). Le grandezze AB e BD non possono dunque avere una comune unità di misura!

Questa conclusione porta, in altre parole, all’ “incommensurabilità” e il punto perde qualsiasi dimensione dato che, in caso contrario, sarebbe stato una comune unità di misura il che abbiamo visto impossibile. Esso è quindi un ente razionale solo pensabile nella sua astrazione e da ciò segue la geometria razionale. quella geometria che noi siamo abituati a studiare; i numeri interi quindi non sono sufficienti ad esprimere tutta la matematica. Ma questo coinvolge l’intera concezione dell’Universo sino ad allora basata, come abbiamo visto, sul numero intero.

Dopo un ragionevole smarrimento si cercò di ovviare in vari modi alla presenza insopprimibile dell’incommensurabilità costruendo serie approssimanti "radice di 2" ("numeri diagonali e laterali"), abbandonando in molti casi i numeri privilegiando la geometria ma anche accettandone la presenza. Ad esempio il pitagorico Filolao (˄ 470 a. C.) asserisce (secondo quanto riporta Stobeo) che «necessariamente le cose sono o tutte terminanti o tutte interminate o terminanti e interminanti insieme». Sembra di vedere Filolao che osserva un segmento terminato nella sua lunghezza ma interminato nell’insieme dei punti che lo costituiscono.

Cosa avrebbe detto Filolao o chi per lui se, grazie alla corrispondenza biunivoca di due insiemi avrebbe saputo che, ad esempio, i numeri quadrati hanno la stessa numerosità di tutti i numeri naturali?

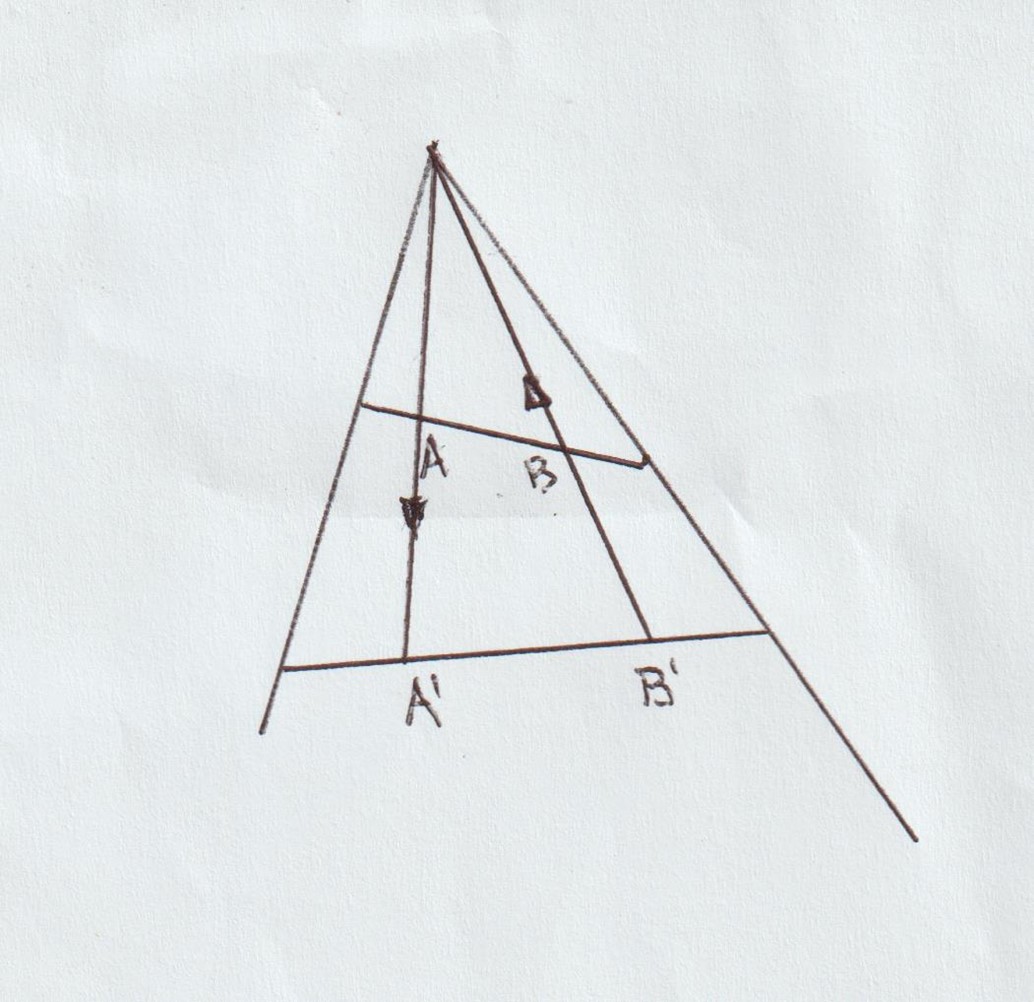
D’altra parte nella matematica ormai diventata razionale, capita che due segmenti di lunghezza diversa abbiano, come indicato nella figura, uguale numero di punti avendosi tra essi una corrispondenza biunivoca (ad ogni punto A di un segmento corrisponde un determinato punto A’ nell’altre e viceversa a B’ corrisponde B)

Si dovrebbe ora ricordare in qual modo i matematici greci reagirono alla presenza dell’infinito creando, ad esempio, approssimazioni notevoli della  (“numeri diagonali e laterali”), oppure usufruendo di procedimenti che anticipavano la teoria dei limiti (metodo di esaustione”), ma usciremmo dal tema del presente articolo limitandomi soltanto ad indicare ove trovare tali sviluppi il volume Attraverso la storia della matematica di Attilio Frajese  (Le Monnier, 1969).

ALTRE PROPRIETA’ DEI NUMERI

Si ha un numero primo se i suoi divisori sono solo l’unità e se stesso. Ad esempio sono numeri primi: 2 (unico numero primo pari); 3; 5; 7; 11; 13; 17 ecc.. Ebbene , una delle più belle dimostrazioni di ogni tempo è quella in cui Euclide dimostra la infinità dei numeri primi (prop. 20 del libro IX). La dimostrazione, che qui non poniamo, mostra che se essi si considerassero un insieme finito si potrebbe dimostrare che ne esisterebbe sempre un altro non appartenente all’insieme.

Nonostante molteplici tentativi di matematici grandi e piccoli, non è stata mai trovata una formula che potesse individuare questa infinità come avviene, ad esempio, per i numeri dispari o, come sappiamo, per i numeri quadrati. Dobbiamo limitarci o al procedimento di Eratostene (trovato un numero primo cancellare tutti i suoi multipli) o verificare caso per caso la sua primitività.

Legati ai numeri primi sono i cosiddetti “numeri perfetti” cioè quei numeri uguali alla somma dei suoi divisori minori del numero stesso, quale ad esempio 6 = 1+2+3 oppure 28 = 1+2+4+7+14. Di questi numeri non si sa né se esistono numeri perfetti dispari, né se essi sono infiniti. Sappiamo però che se il numero 2ⁿ -1 è numero primo, allora il numero 2^n-1(2ⁿ -1 ) è numero perfetto; questa condizione sufficiente si deve ad Euclide (Elementi IX,36) e la necessaria ad Eulero (cfr. Dickson, History of theory of numbers, I, New York 1934, p.19).

Notiamo infine che grazie all’uso dei “fattoriali” è possibile trovare intervalli di numeri grandi a piacere (10; 100; 100.000 cento miliardi ecc.), privi di numeri primi !

Al termine di questa conversazione, riprendendo le attribuzioni quasi divine attribuite al numero, riporto la premessa ad un testo matematico:

Regole per studiare la natura e conoscere tutto ciò che esiste, ogni mistero, ogni segreto. (Premessa al papiro Rhind, 1600 a.C. circa)

I dotti egiziani avevano già capito tutto.

 

Silvio Maracchia  

 

^[1] Per la numerazione sumera si veda ad esempio il secondo capitolo della mia Storia dell’algebra (2^a ed. 2008, Liguori, Napoli).