Tabellina pitagorica: le spirali pitagoriche
Molti anni fa un bambino mi fece una domanda “Che c’entra la tabellina pitagorica con il Teorema di Pitagora?” Al di là della classiche operazioni, sempre utili, e una probabile origine comune, pensai, non molto. Ma dopo parecchi anni, una cinquantina, ho capito che quel bambino aveva intuito qualcosa di molto interessante, ma perso nei secoli.
Quindi oggi dimostreremo, seguendo un metodo molto antico, la connessione tra le tabelline pitagoriche (praticamente qualsiasi tabellina, dalla classica 10x10, alle più piccole, e volendo alle più grandi) ed il Teorema di Pitagora.
Anzi dimostreremo che da una classica tabellina:
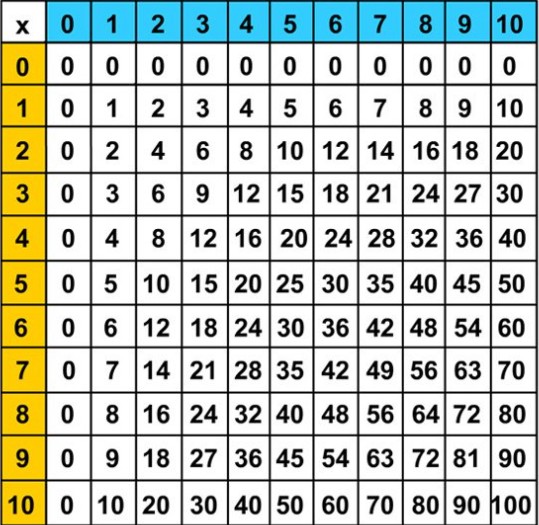
Fig. 1
Possiamo costruire geometricamente delle spirali pitagoriche, del tipo:
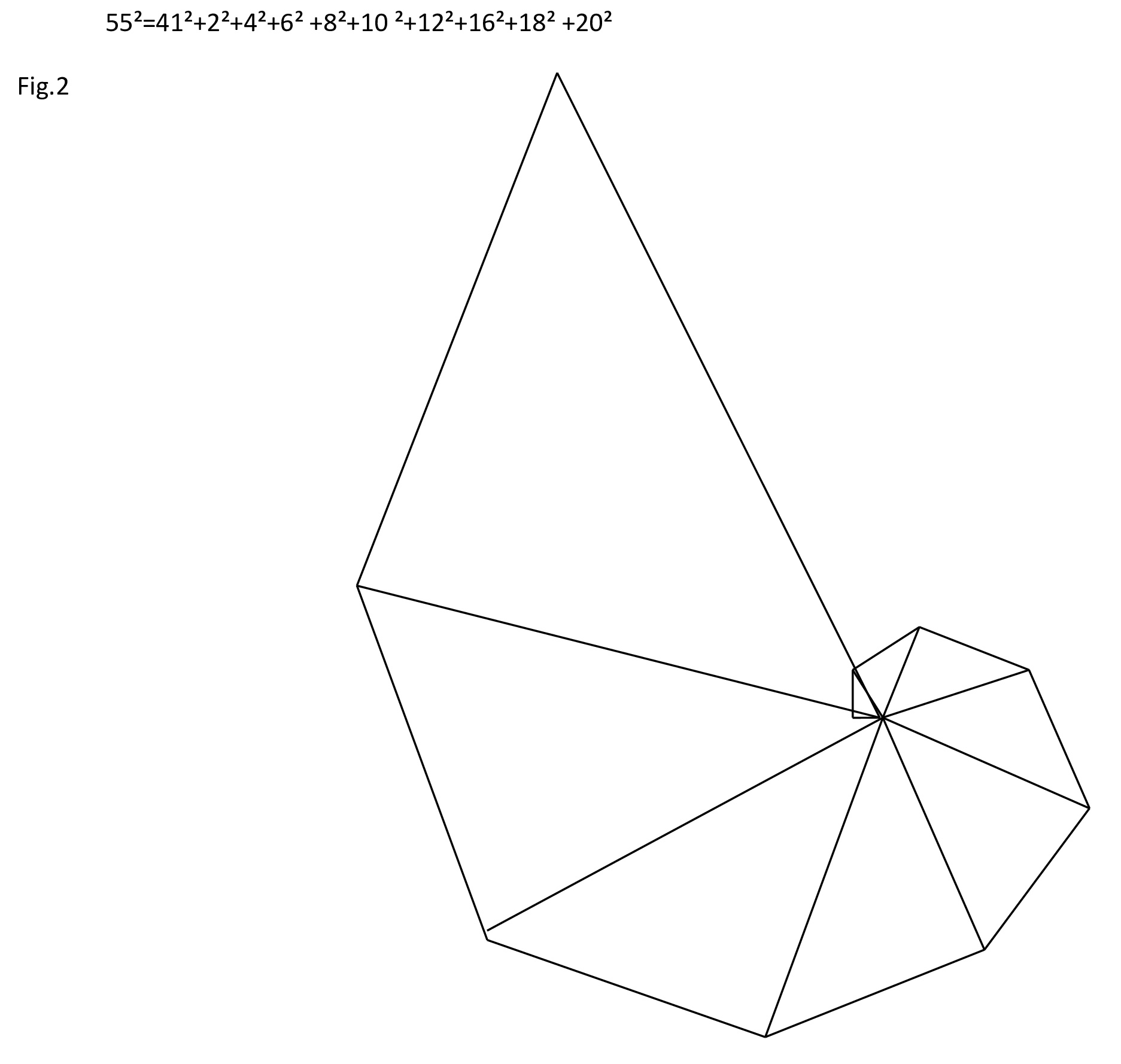
Fig. 2
Per arrivare a comprendere ciò dobbiamo partire dall’origine, o almeno da uno spartiacque, che si condensa in Euclide e nei suoi Elementi. L’antica tradizione matematica egizia, babilonese e poi pitagorica, veniva rinnovata, da quello che allora era il pensiero moderno: la geometria euclidea. I suoi cinque postulati, le dimostrazioni, la squadra, il compasso, preposizioni, solidi geometrici, il continuum rispetto al discreto, ecc. ecc., le fondamenta della nostra matematica. Cose che da più di 2000 anni, qualsiasi giovane studente deve affrontare e su cui si forma le proprie basi matematiche. Visto che, invece, la radice di questo studio si basa su un’aritmogeometria pre-euclidea, non vi chiedo di dimenticare Euclide, ma di provare ad avere una visione un po’ più amplia da come ci siamo formati ed abituati. La cosa interessante è che è proprio Euclide che ci fornisce l’elemento base ed indispensabile per indagare tale metodo pre-eucildeo. Nel libro X degli Elementi lemma 1 prep. 29, in sintesi abbiamo un metodo per trovare tutte le terne pitagoriche, partendo da due soli numeri: m, n (meglio se un pari ed un dispari e non multipli tra loro, almeno per le terne primarie): a=m²-n², b=2mn, c=n²+m².
Apparentemente un giochino di curiosità matematica. Va detto che pochi secoli dopo viene ripreso da Diofanto nel suo prealgebra ellenico e successivamente da matematici arabi, nonché da Fibonacci ed altri italiani, l’ultimo a considerarlo fu Fermat, ma, proprio in quel periodo, con Cartesio, nasceva l’analisi matematica e fu completamente abbandonato. Va aggiunto che Euclide non andò troppo in profondità, ci dà una dimostrazione numerica, che ha le basi nelle proporzioni del libro IX, sempre di radice pitagorica, senza però alcuna relazione ai triangoli rettangoli, né tantomeno con il Teorema di Pitagora, tant’è che oggi se parliamo con un matematico sembra che le terne pitagoriche non abbiano molto a che vedere con il Teorema stesso. Evidentemente questo metodo, nel bacino del Mediterraneo, doveva avere avuto un’origine pitagorica, anche se oggi sappiamo che la sua radice primaria è babilonese (varie tavolette d’argilla in cuneiforme ne attestano la provenienza, come la Plimpton ed altre più recentemente trovate e comprese).
Oggi la dimostrazione più semplice è di tipo algebrico, con questa uguaglianza:
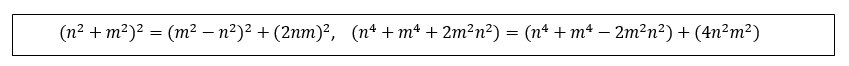Formula 1
In prima istanza andiamo a vedere come funziona questo metodo piuttosto elementare, al contempo lo osserveremo attraverso le relazioni storiche e filosofiche del suo tempo e cercheremo di dare delle dimostrazioni più scientifiche nel senso moderno. Partiremo dalla tabellina più semplice quella del 2, che sarebbe più corretto dire quella formata da due numeri, appunto n ed m:
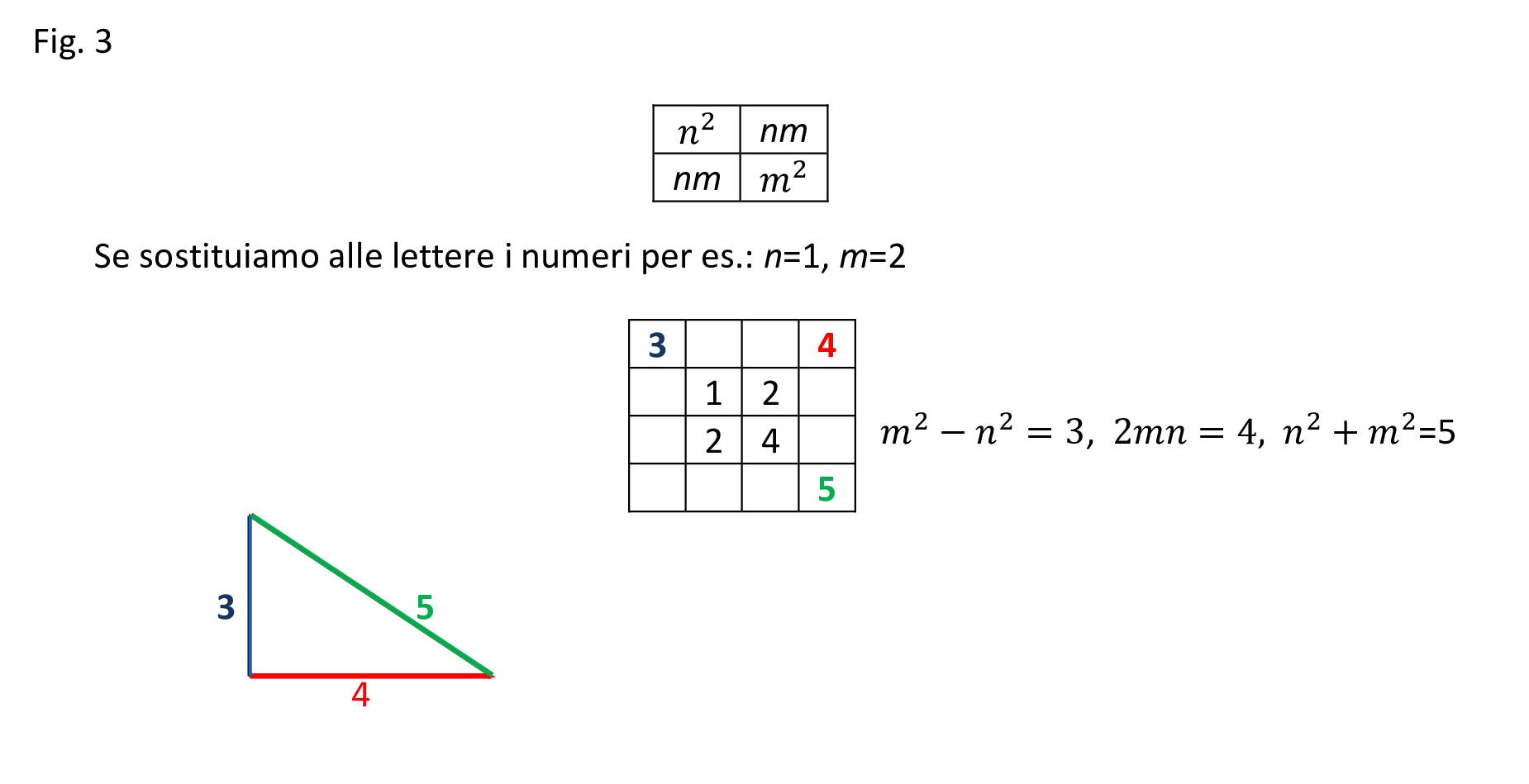
Fig. 3
In origine la rappresentazione grafica di quello che oggi definiremmo il quadrato di un binomio: (m+n)²=m²+2mn+n² , era basata su un’aritmogeometria tassellata, ma quando i Greci ed in particolare i pitagorici approfondirono la geometria venne preferita la rappresentazione in tabellina. Questo crediamo per non confondere i numeri, intesi come archetipi, dai numeri di misura, o se preferiamo i numeri di qualità da quelli di quantità.
Di fatto però a=m²+n², b=2mn, c=n²+m², viene esplicato in: c²=a²+b².
Tutto ciò permette per qualsiasi n ed m di costruire infinite terne pitagoriche (meglio se un pari e un dispari, cioè un femminile ed un maschile, infatti il Teorema di Pitagora era anche detto degli sposi o del matrimonio). In pratica da una banale tabellina di due numeri qualsiasi, noi sommiamo i quadrati ed abbiamo il valore dell’ipotenusa c, facciamo la sottrazione degli stessi quadrati ed abbiamo il valore del cateto di ordine dispari a, mentre con il doppio prodotto abbiamo il valore del cateto di ordine pari b. Oppure, se preferite, da un banale quadrato di un binomio se sommiamo i due quadrati abbiamo c, se ne facciamo la differenza abbiamo a, mentre con il doppio prodotto abbiamo b. Una sorta di magia, ma abbiamo visto dalla formula algebrica di Form. 1, che è una proprietà insita in tutti i numeri. Solo che è difficile da inserire in una dimostrazione prettamente geometrica, poiché dal punto di vista geometrico, delle aree, però numeriche, diventano, poi, dei segmenti (cateti ed ipotenusa). Possiamo in questo senso comprendere la riluttanza di Euclide nel collegare tutto ciò nella genesi del Teorema di Pitagora, dovendo lui forgiare una geometria che non ammettesse dubbi; il numero doveva rappresentare una misura matematico geometrica sicura. D’altronde pochi anni prima Aristotele dal dialogo Sulla Filosofia: “Se le idee sono un’altra specie di numeri, diversa da quella matematica, noi non possiamo averne intendimento. Chi infatti, almeno nella maggior parte di noi, può intendere che cosa sia un numero di specie diversa?”
Seppure, alcuni secoli dopo, ci ispirano ancora alcuni passi di Plutarco e Proclo, essi narrano che Pitagora sacrificò agli dei un bue in onore di una acquisizione del sapere umano: o per il Teorema di Pitagora o per l’Applicazione delle Aree, aggiungendo che quest’ultima sarebbe stata più gradita dalle Muse. Strano perché pensiamo tutti che se Pitagora dovesse offrire un sacrificio agli dei dovesse essere per il suo teorema. Ma la nostra tesi è che Pitagora sacrificò il bue e per il Teorema di Pitagora e per l’applicazione delle aeree, perché in questo ambito convergono, ovvero sono una cosa sola, esprimibile in diversa modalità (una geometrica, l’altra arcaica, anche se oggi diremmo di base algebrica). Solo che quel genere di applicazione di aeree doveva essere espunto dall’applicazione delle aeree come ce l’ha tramandata Euclide, perché non aveva senso geometrico, o almeno poteva creare una gran confusione. Molto probabilmente i pitagorici passarono da una forma aritmogeometrica atavica (mesopotamica) alle tabelline, proprio per evitare una confusione con la geometria greca, che si stava dispiegando. Diremmo che in partenza era una sorta di pre-algebra figurato, ripreso e depurato poi da Diofanto, che evitò di trattarlo in forma aritmogeometrica. Perdurò nel bacino del Mediterraneo, come sapere esoterico, e le tabelline (senza per questo sconfessare il valore aritmetico della tabellina in se) ne sono una traccia.
Il problema è che anche tutti noi siamo post euclidei e quando dico ad un matematico che l’ipotenusa è sempre una somma di due quadrati ecco che “Eresia!!! Il quadrato dell’ipotenusa è la somma di due quadrati!” Il fatto è che sono tutte due cose vere, solo che una guarda la trama, l’altra l’ordito. Se tutto quello che diciamo ha ragione d’essere, l’antico metodo dovrebbe funzionare anche per polinomi. Se applichiamo la stessa regola ad un trinomio, quindi ad una tabellina di tre numeri, con le giuste accortezze, invece di un triangolo rettangolo potremo costruire un quadrilatero in cui il lato maggiore avrà una similitudine con l’ipotenusa di un triangolo rettangolo, cioè il quadrato di esso, sarà uguale alla somma dei quadrati dei tre lati del quadrilatero. :
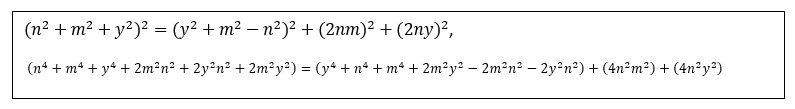
Formula 2
Infatti il risultato è sempre lo stesso, solo che qui la somma dei tre quadrati della tabellina (c “ipotenusa”) elevati al quadrato, sarà uguale al quadrato della differenza tra i quadrati stessi (a), sommato con i doppi prodotti, relativi al quadrato sottratto:
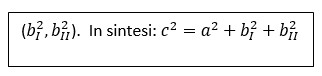Formula 3
La visualizzazione della tabellina chiarisce il sistema.
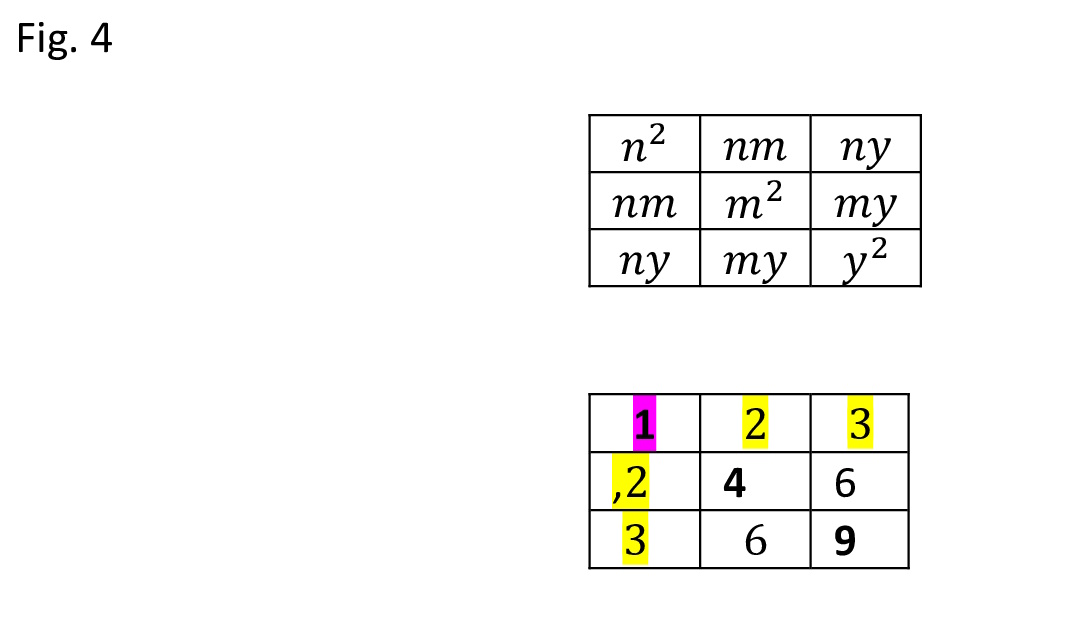
Fig. 4
La somma dei quadrati è 14, la differenza con il primo quadrato (9+4-1) è 12, i doppi prodotti relativi al quadrato di 1 sono 2x2 e 3x 2 (sulla riga relativa al quadrato di 1 e colonna sempre di 1).
Quindi:
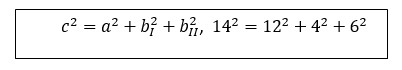Formula 4
quando c è pari, tutti i numeri si potranno dividere almeno per 2, quindi: 7²=6²+2²+3² , 49=36+4+9, che possiamo rappresentare:
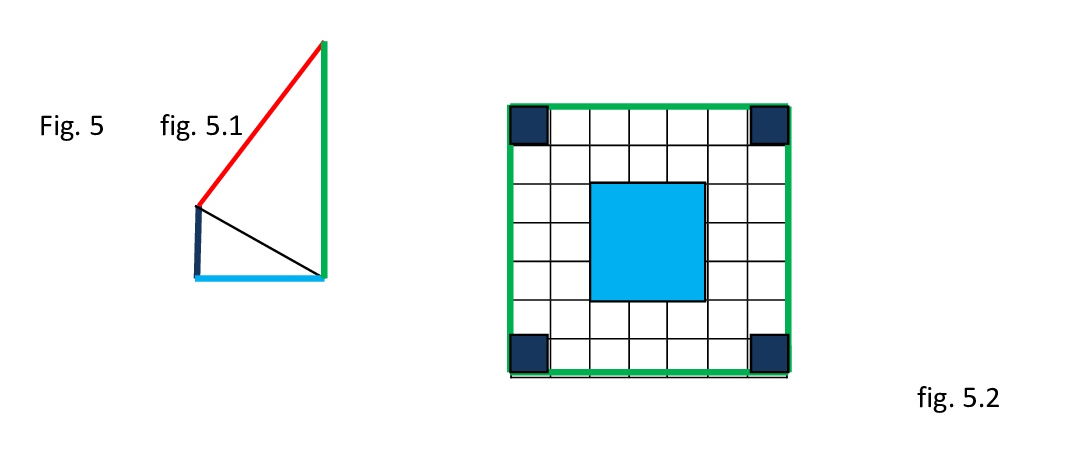
Fig. 5
Nel primo disegno (fig. 5-1) abbiamo un quadrilatero irregolare (costruito da due triangoli rettangoli, che come vedremo nella maggior parte dei casi non appartengono a terne pitagoriche primarie o secondarie classiche) in cui la somma dei quadrati dei tre lati minori è equivalente al quadrato costruito sul lato maggiore, che anche se non propriamente corretto, potremmo chiamare convenzionalmente l’ipotenusa del quadrilatero (di fatto è l’unico ipotenusa che compare unendo i due triangoli).
Nella fig. 5-2: una possibile dimostrazione primitiva, oltre a quella algebrica, la possiamo mostrare attraverso una aritmogeometria tassellata (chiaramente avevamo già diviso per due altrimenti dovevamo partire da un 14x14), in cui tutto il quadrato (contornato di verde 7x7), corrisponde al quadrato dell’ipotenusa, il quadrato turchese ed i quattro quadratini blu, corrispondono a
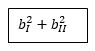
quindi 9 e 4 (sommati 13); mentre i quadratini lasciati in bianco ad
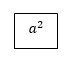
49-13=36 (e si possono elementarmente contare dalla tassellatura). In questo caso, potete provare, se invece di togliere il quadrato di 1 alla somma dei quadrati, togliamo quello di 4, oppure quello di 1 e di 4 sommati, il risultato non cambia. Cioè avremmo sempre la stessa equazione, quindi anche le stesse figure. Ma se vogliamo lavorare almeno fino alla tabellina pitagorica (10x10), dobbiamo vedere il metodo in altre situazioni. Ad esempio:
Fig. 6
Quindi avremo tre quadrilateri differenti in cui comunque il quadrato del lato maggiore, 529, sarà uguale alla somma dei quadrati degli altri lati. Stessa cosa per la rappresentazione tassellata. D’altronde come esistono infinite terne pitagoriche così anche per le quaterne (pitagoriche).
La stessa cosa avviene se assumiamo come base aritmogeometrica arcaica un quadrato di un polinomio di 4 numeri o la tabellina del 4 ( ma, vedremo, anche molti di più ):
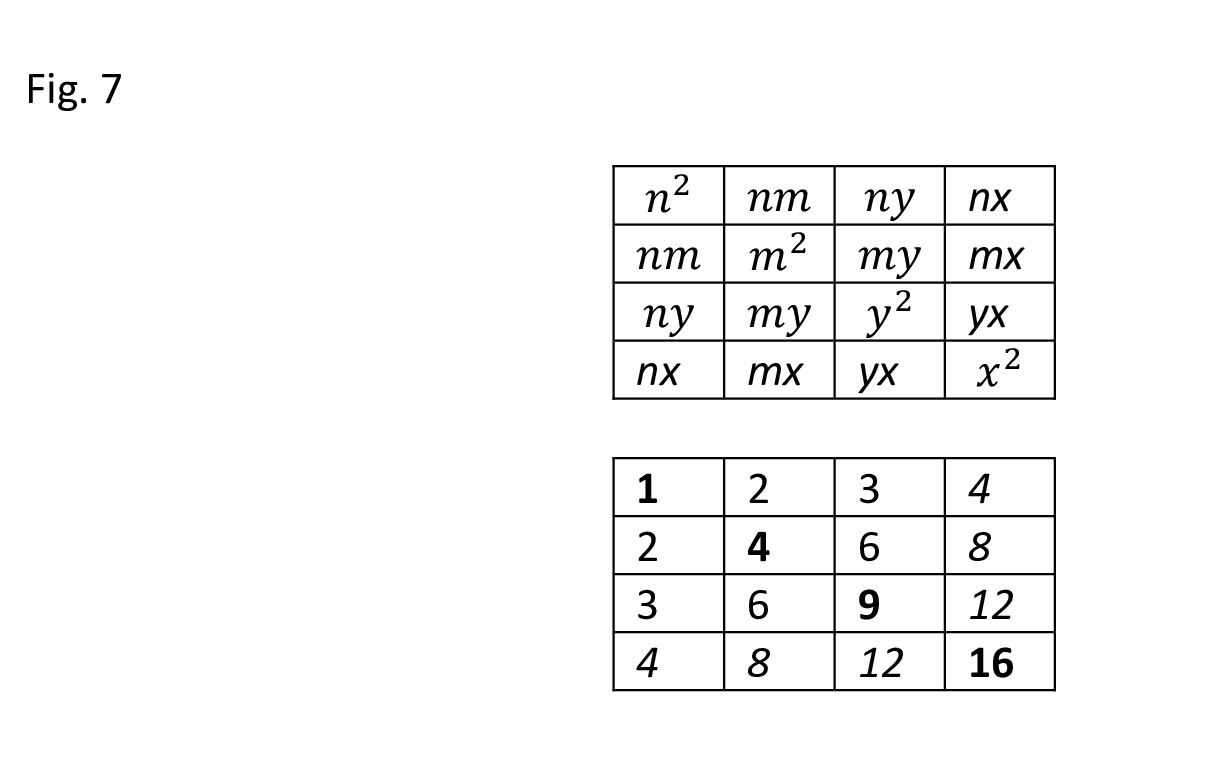Fig. 7
Anche qui come vedremo si andranno a formare cinquine pitagoriche, ma mentre con il quadrato di un binomio possiamo formare una solo terna pitagorica, e con il quadrato del trinomio 3 quaterne pitagoriche. Vedremo che qui il numero delle cinquine è maggiore:
Fig. 8
Quindi abbiamo 4 cinquine e 3 sestine pitagoriche, che poi geometricamente ci porta alla costruzione di 7 poligonali chiuse (4 pentagoni irregolari e 3 esagoni irregolari):
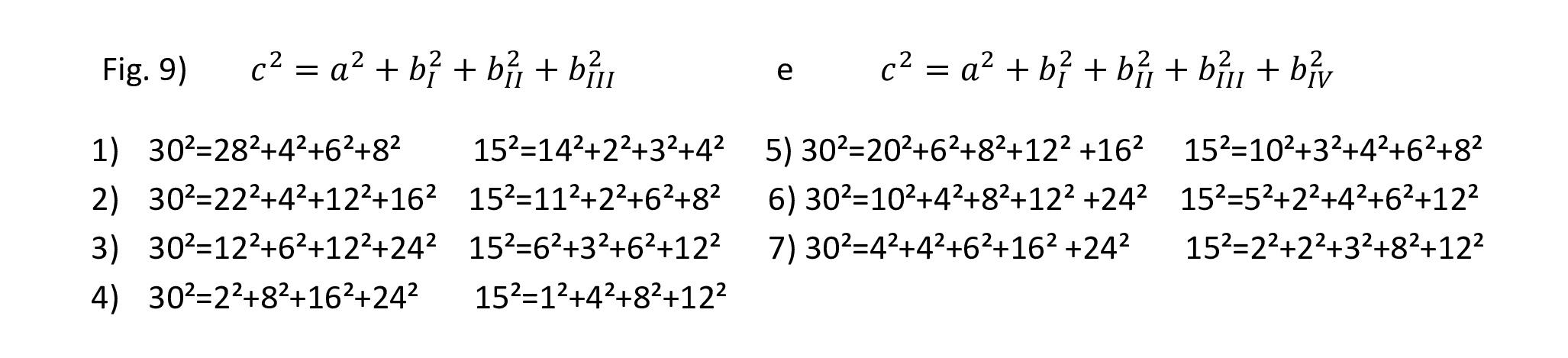Fig. 9
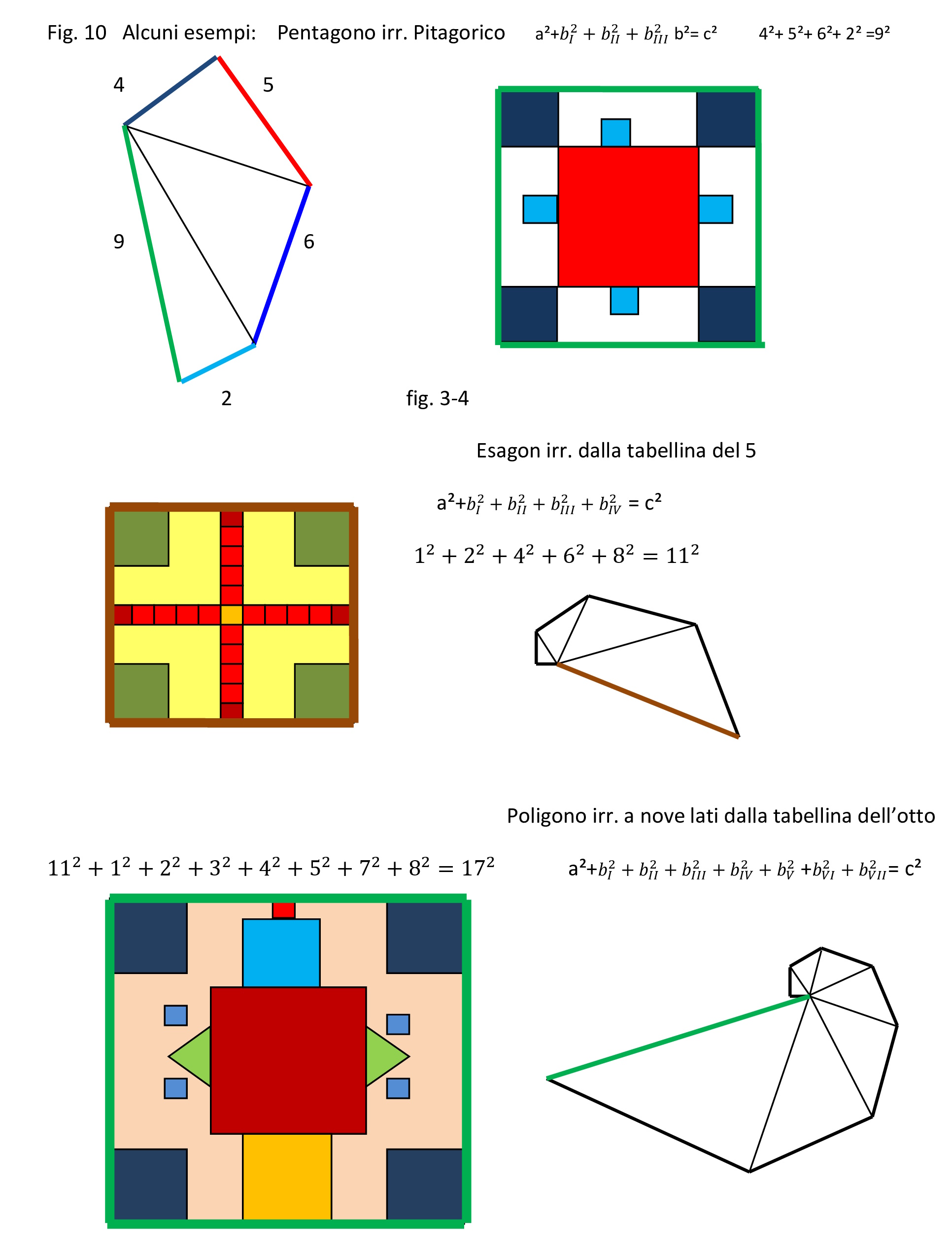Fig. 10
Potremmo proseguire all’infinito avremo sempre un quadrato (del lato maggiore: “ipotenusa”) eguale alla somma di tutti i quadrati dei lati di qualsiasi poligonale. Il metodo di base è sempre lo stesso: somma di tutti i quadrati della tabellina e avremo il lato “ipotenusa”, differenza di uno o più quadrati dalla somma totale ed avremo il lato a, doppi prodotti tra la riga e la colonna relative al quadrato tolto ( o dei quadrati tolti) per a ed avremo i vari b. Si potrà obiettare che legando tre terne classiche 3, 4, 5 con 5, 12, 13 e con 13, 84, 85 e quindi unendo i tre triangoli rettangoli possiamo avere una cinquina pitagorica. Infatti è giusto, ma osservandola da questo punto di vista è solo un caso particolare di una tabellina di 4 numeri o se vogliamo di un particolare quadrato di un quadrinomio:
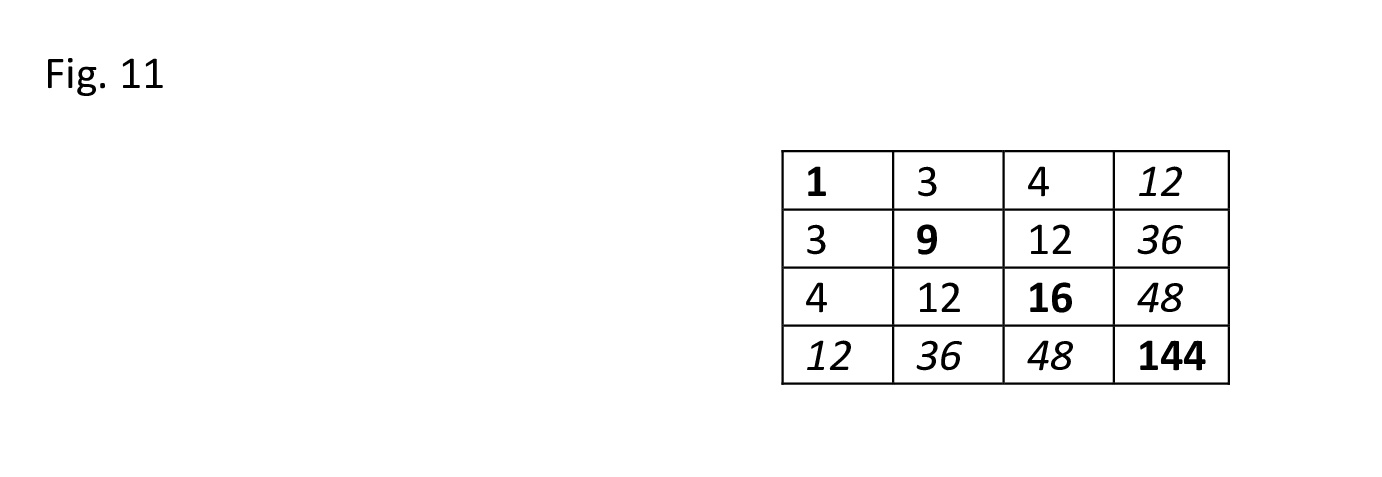Fig. 11
La somma dei quadrati è 170, (tutto divisibile per 2), quindi “ipotenusa”=85 ed abbiamo queste cinquine:
3-4-12-84-85 appunto, ma anche 3-12-36-76-85, come 4-12-48-69-85, e 12-36-48-59-85, e come sestine:
4, 12, 12, 36, 75, 85 - 3, 12, 12, 48, 68, 85 e 3, 4, 36, 48, 60, 85. A differenza della prima cinquina le altre (e tutti gli infiniti casi che vedremo) hanno gli ipotenusa intermedi (della serie di triangoli rettangoli che vanno a comporre il poligono irregolare) generalmente in numeri irrazionali.
La cosa interessante, è che più la tabellina, il polinomio, si ingrandisce, più si va verso delle forme geometriche che tendono alla spirale logaritmica.
Facciamo un esempio:
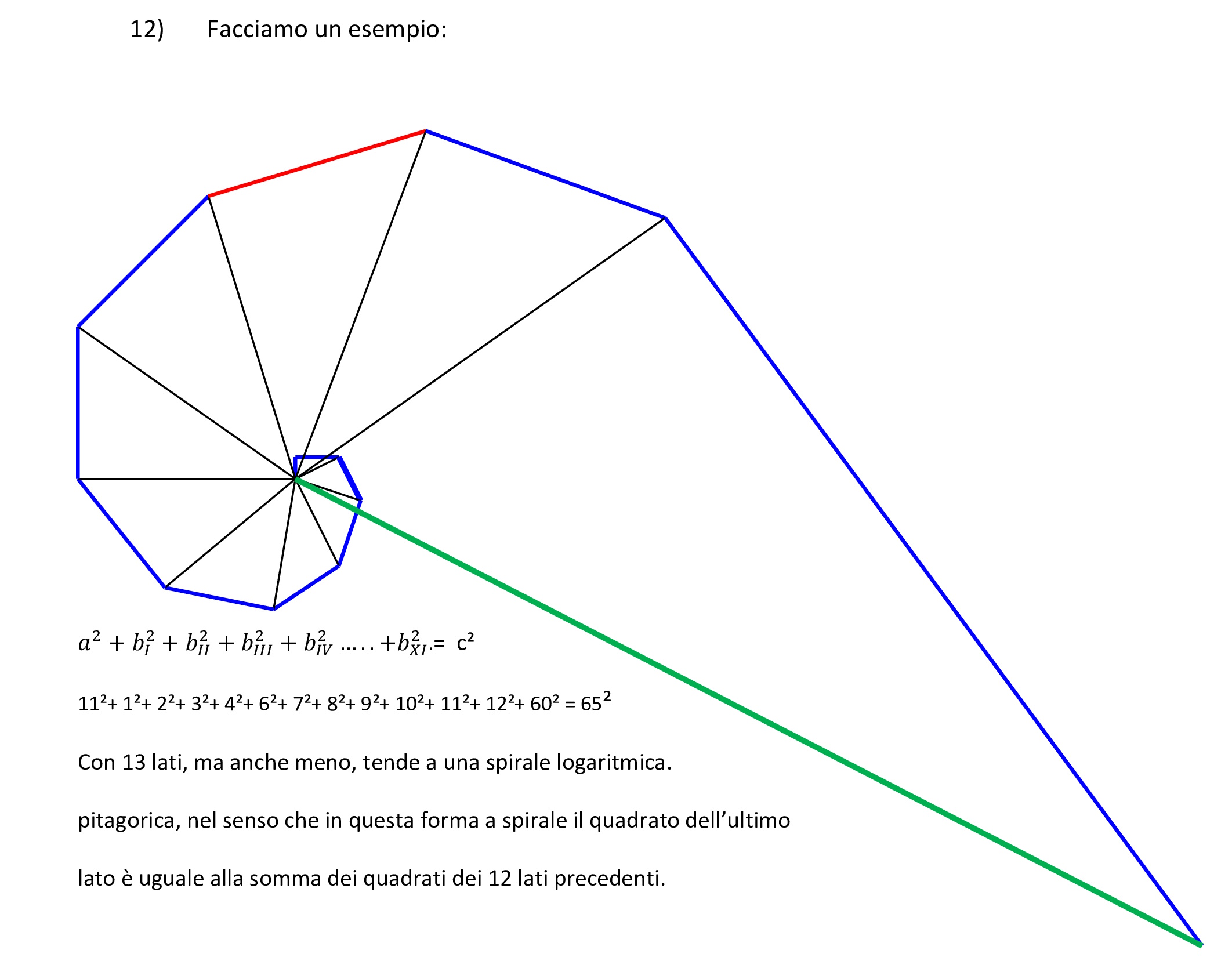Fig. 12
Chi si vuole divertire può passare alla tabellina del 5 che ha almeno 15 soluzioni, poi del 6 del 7 fino ad arrivare a 10 e più. Adesso possiamo provare ad osservare la tabellina pitagorica da questo punto di vista.
Fig 13
Quindi nella maggior parte dei casi abbiamo 9 doppi prodotti, una somma di tutti i quadrati ed una differenza di un quadrato (iniziamo a sottrarne solo uno), come risultato abbiamo undicine pitagoriche che possono costruire geometricamente poligoni irregolare ad 11 lati appunto, in cui il quadrato costruito sul maggiore è uguale alla somma dei quadrati degli altri dieci.
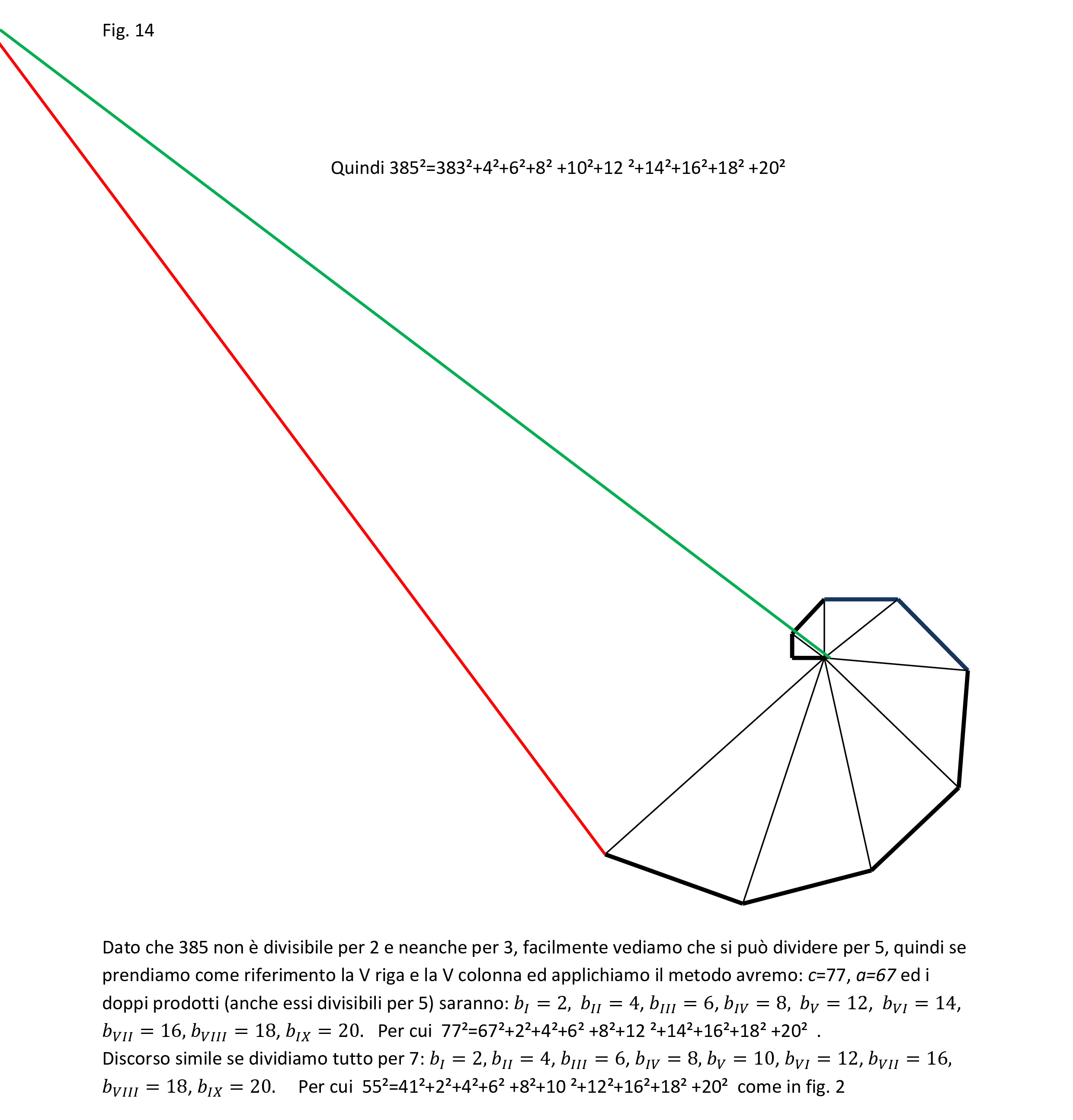Fig 14
Ora però con la tabellina pitagorica a seconda di quanti quadrati sottraiamo dalla somma avremo differenti lati a ed un numero maggiore di doppi prodotti, l’esempio più semplice da mostrare visto che 385 è divisibile per 5, lo abbiamo prendendo in sottrazione i quadrati di 5 ed di 10, entrambi divisibili per 5 (così anche i loro doppi prodotti).
Fig. 15
Per cui 77²=27²+2²+4²+4²+6² +8²+8²+12 ²+12²+14²+16²+16²+18² +24² +28² +32²+36².
Abbiamo quindi un poligono irregolare con 18 lati, in cui il quadrato del lato maggiore è equivalente alla somma dei quadrati degli altri 17 lati. Possiamo aggiungere che noi lo disegniamo con i lati in ordine crescente, ma a parte l’ultimo (“ipotenusa”), gli altri si possono ordinare a nostro piacimento perché il risultato non cambia.
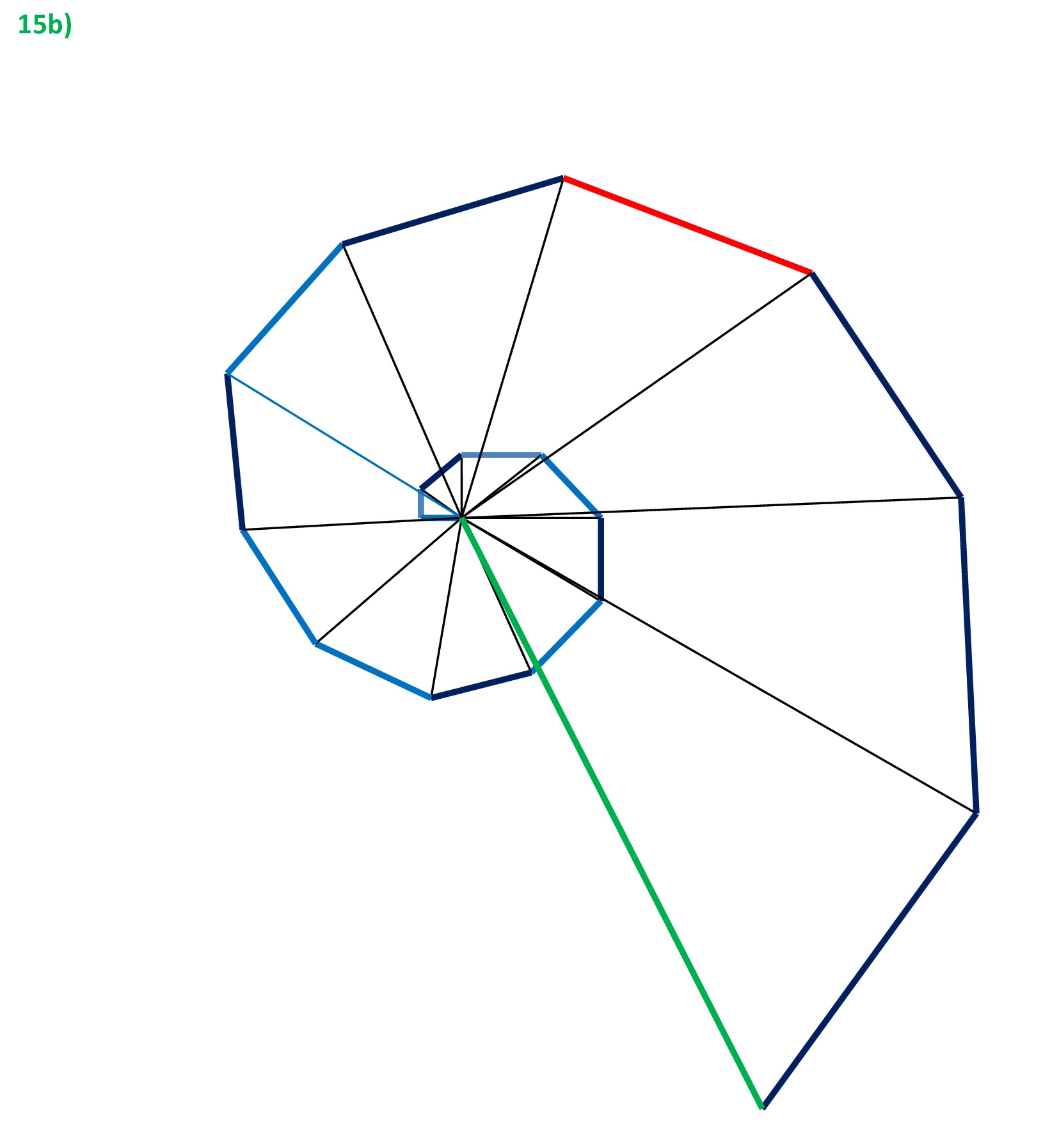Fig 15b
77²=27²+2²+4²+4²+6² +8²+8²+12 ²+12²+14²+16²+16²+18² +24² +28² +32²+36². Le misure del disegno non sono perfette ma si avvicinano con una certa approssimazione alla figura geometrica in scala data dalla formula, che abbiamo ottenuto dalla Tabellina Pitagorica.
Il massimo dei lati che possiamo produrre con questo metodo dalla classica Tabellina Pitagorica è di 27. Prendiamo i quadrati di 1, 2, 3, 4 e 5 e li sottraiamo alla somma degli altri avremo come differenza 275, poi prendiamo i doppi prodotti relativi ai cinque quadrati predetti ed avremo:
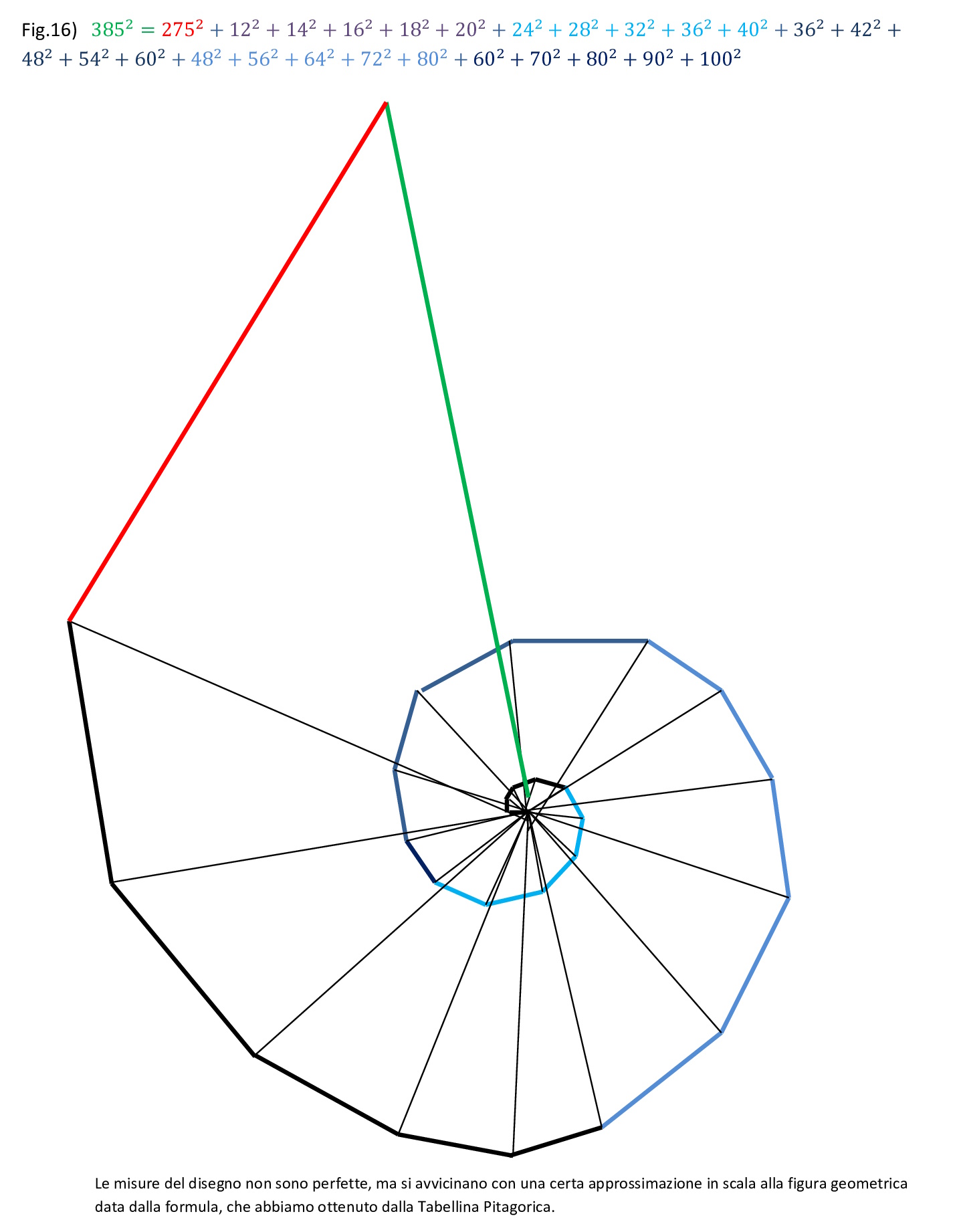Fig. 16
Conclusioni: Abbiamo visto che esiste un metodo che permette di costruire poligoni irregolari, in cui il lato maggiore, che chiamiamo ipotenusa (anche perché di fatto è l’unico ipotenusa che compare nella figura costruita da vari triangoli rettangoli), al quadrato è uguale alla somma dei quadrati di tutti i lati della figura. Il metodo si basa sul lemma 1 prep. 29 libro X degli Elementi di Euclide, espandendolo all’infinito.
Quindi da:
Fig. 17
Certo è una matematica molto antica, una matematica del discreto, ma, se i pitagorici avevano una qualche ragione, è una matematica che dovrebbe rispettare la Natura e l’Armonia delle cose.
Non a caso è la stessa matematica che usò Gregory Mendel per mostrare alcune leggi basilari della genetica di tutti gli esseri. Per es. fenotipo per due alleli: pisello giallo o verde, come n ed m per la tabellina del 2 o se preferite per il quadrato del binomio (con tre alleli useremmo la tabellina del 3 e così via; con dieci alleli sarebbe analogo alla tabellina pitagorica):
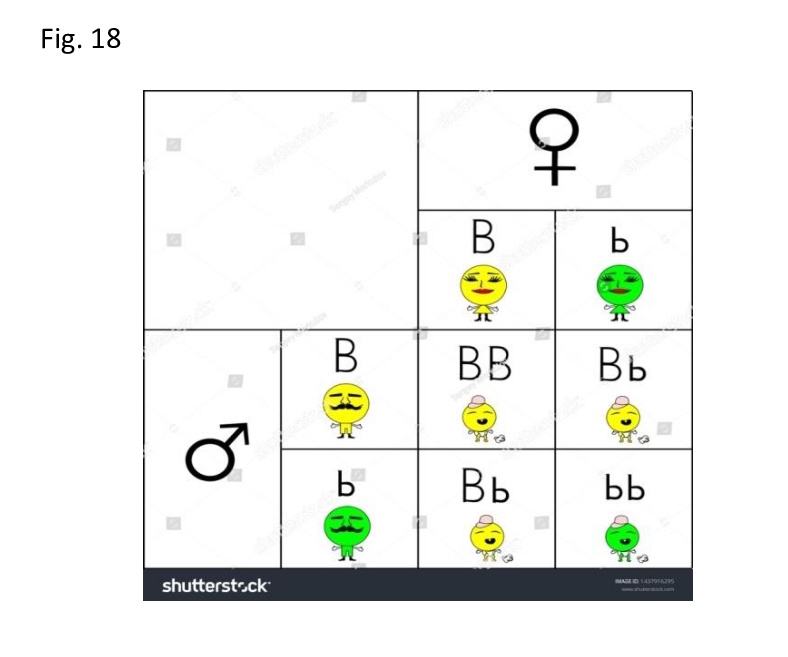Fig. 18
La Spirale aurea
Sul tema dell’Armonia e della Natura. Applicando lo stesso metodo su una tabellina del 12x12, ma se invece di porre i primi dodici numeri, mettiamo questi altri: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144. Cioè i primi 12 numeri della serie di Fibonacci possiamo costruire una spirale aurea: (1²+1²+2²+3²+5²+8²+13²+21²+34²+55²+89²+144²)²= (1²+2²+3²+5²+8²+13²+21²+34²+55²+89²+144²-1)²+ 2²+4²+5²+10²+16²+26²+42²+68²+110²+178²+288². Dato che la somma di tutti i quadrati è divisibile per due: 33552, si possono dividere per due tutti gli altri. Avremo tutti i lati (della lunga serie di b) della nostra spirale, eccetto quindi a e c, in completa serie di Fibonacci.
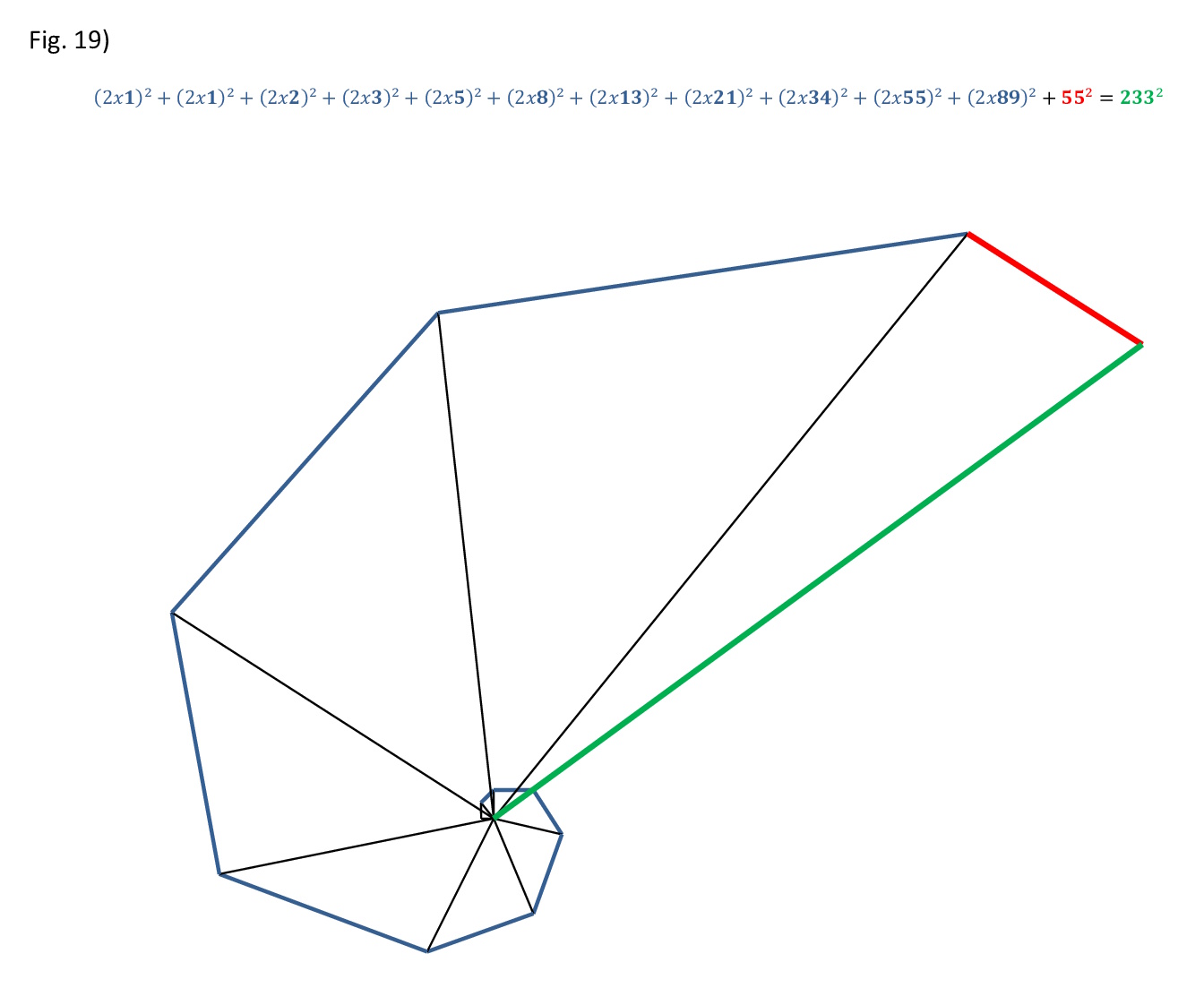Fig. 19
Tra le proprietà della serie di Fibonacci ne abbiamo una che ci aiuta molto nel costruire spirali auree: se prendiamo due numeri in successione x ed y, possiamo osservare che il loro prodotto è sempre uguale alla sommatoria dei quadrati da 1 ad x.
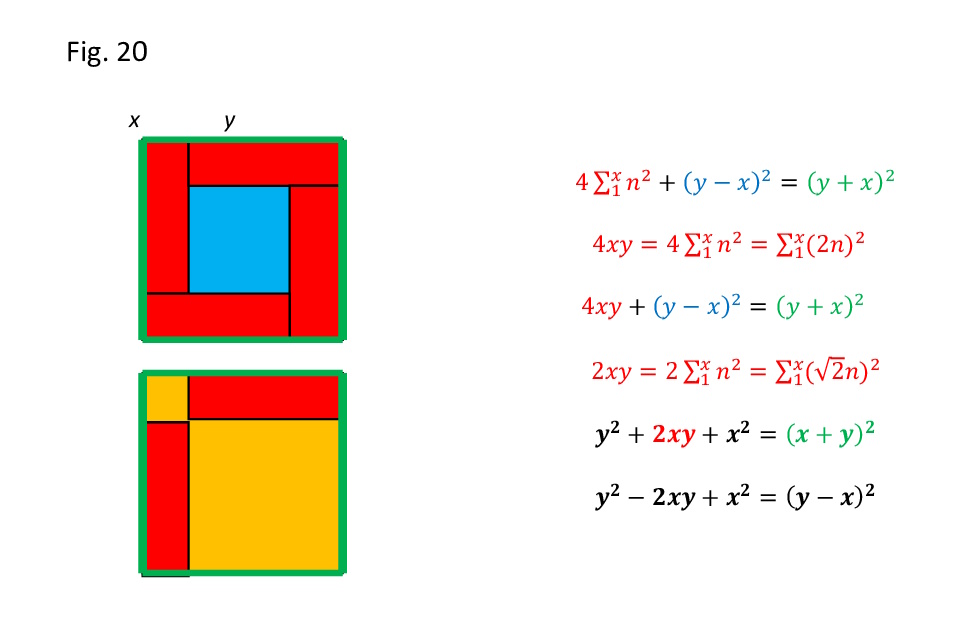Fig. 20
In altre parole la somma dei quadrati della serie fino ad x è uguale al prodotto xy. Es. x=5 y=8
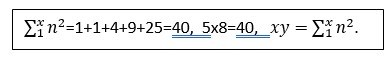
Formula 5
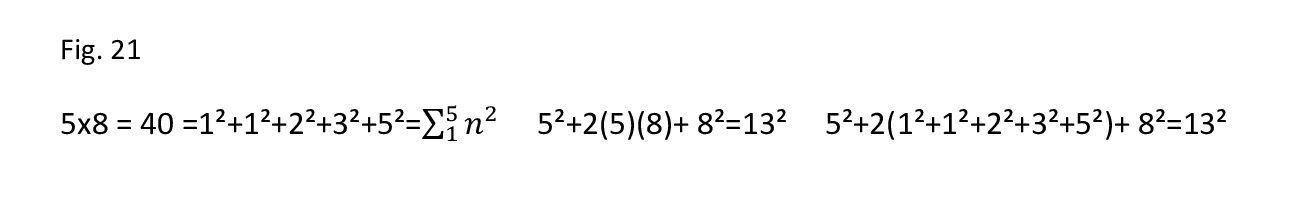Fig. 21
Questo ci torna molto utile per costruire spirali auree di grandi dimensioni, es. x=89, y=144:
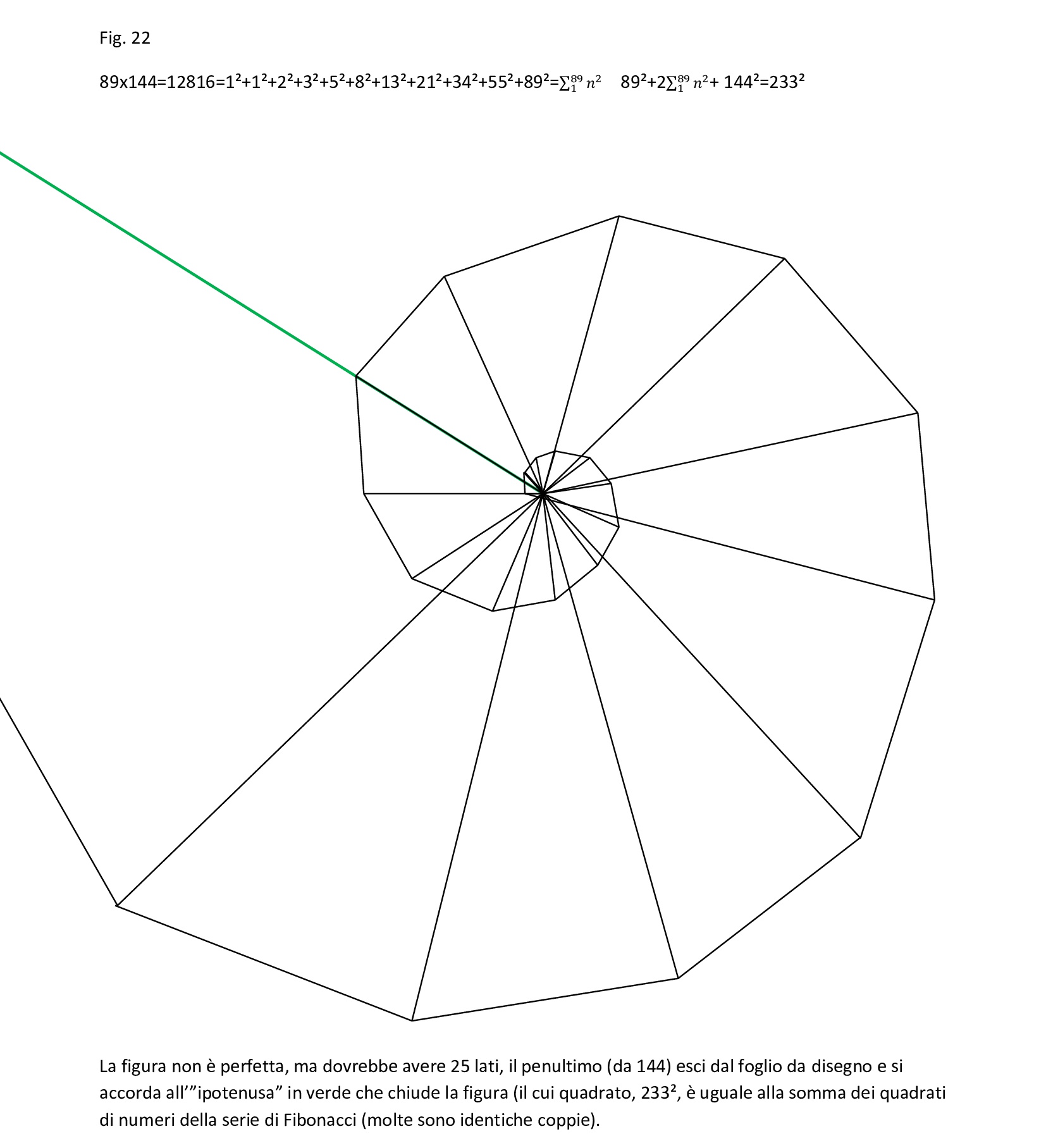Fig. 22
