Premessa.
Uno degli aspetti più interessanti della lunga amicizia tra un matematico con un’anima filosofica e poetica come Silvio Maracchia e un anima metafisica, come quella del sottoscritto, prestata alla tecnologia è l’apertura di strane discussioni tra noi nelle quali dei principi religiosi dilagano dentro quella misteriosa e nebulosa sezione della matematica che si interessa di “indeterminato”, “infinito”, “insiemi”, “frattali” ecc.. In tali sezioni alcuni assiomi, anche se governabili tramite algoritmi, lasciano spazio a molte perplessità sul senso e sulla dimostrabilità. Ad esempio come è possibile che i quadrati dei numeri siano tanti quanto i numeri anche se le “distanze” numeriche, tra un numero quadrato e l’altro, comprendono una quantità di numeri superiori a quelli della successione fra i quadrati stessi? In questo breve ma intenso articolo Maracchia propone temi assai arditi anche se apparentemente semplici e tutt’altro che risolti ma che aprono la mente e il cuore verso l’insondabile e costringono anche l’ateo più accanito a dire: “non lo so”. Per tale ragione, ho introdotto in questo articolo un disegno che ho fatto molti anni fa, estratto da una conferenza nella quale mi ponevo, anche se in una chiave diversa, il problema della conciliazione dei tre lati del triangolo formato da due semiassi della croce e la base terrena come ipotenusa, che troverete qui esposto dal prof. Maracchia. Claudio Lanzi
Matematica e religione
Sono molte le perplessità che nascono allorché si vuole dare una spiegazione razionale e coerente ad avvenimenti narrati nella Bibbia e agli sviluppi successivi, sia nel nuovo Testamento e sia nel trascorrere dei secoli. La maggior parte di essi vengono classificati “misteri” che non sono dati a noi conoscere. Il principale di questi è, a mio parere, quello del male, della sua esistenza e del suo perdurare durante i secoli. Si dà una certa spiegazione alla libertà concessa all’uomo e con questo si pensa di aver superato le perplessità sorte a questo proposito. Ma sembra una spiegazione di rimessa, una giustificazione piuttosto.
Dante Alighieri, ad esempio, non nasconde l’esistenza di problemi irrisolti ma in due bellissime terzine risolve quasi sorridendo il problema pensando alla nostra finitezza umana che non consente di valutare l’infinitezza divina dando anche una spiegazione della venuta di Cristo sulla terra (Purg. III; vv. 34-39).
Matto è chi spera che nostra ragione
possa trascorrer la infinita via
che tiene un sustanza in tre persone
State contente, umana gente, al quia;
ché se potuto aveste veder tutto,
mestier non era parturir Maria.
Come possono legarsi tre ”persone” , il Padre, il Figlio e lo Spirito Santo ed essere nello stesso tempo una? Nel Catechismo più volte il concetto di Trinità viene considerato un “mistero” anzi (n. 234) il “mistero centrale della fede e della vita cristiana”, proporzione divina perché una e trina e con la “medesima natura” (253). Vedremo in seguito un spiegazione… matematica.
Luca Pacioli vide nella sezione aurea, e cioè in un segmento diviso opportunamente in due parti (una di queste media proporzionale tra l’intero segmento e la parte rimanente), una suddivisione eccezionale da lui indicata appunto come “sezione aurea”, come ad indicare, in parallelo con la trinità divina, la suddivisione di un segmento (il padre?) in due parti (il figliolo e lo spirito santo?) tale che il suo rapporto con il secondo fosse uguale a quello del secondo con il terzo. Sono tre dunque i segmenti ma si trovano nel maggiore e la sostanza dantesca è data appunto da tre grandezze .
È probabile però che l’eleganza del rapporto tra il segmento e la sua parte aurea (la media proporzionale) che si riscontra nei poligoni e poliedri e, approssimata, nella natura biologica e vegetale, da ritrovarsi anche in alcune famose costruzioni architettoniche, abbia la responsabilità di quel “divina” datole da Luca Valerio. [1]
Parlando però di matematica potremmo avanzare una ulteriore ipotesi che maggiormente potrebbe legarla alla divina Trinità.
Premettiamo però che alcuni studiosi attribuiscono alla nascita della matematica una origine divina. Platone, ad esempio, considera la matematica creazione del dio egiziano Theut e attribuisce al Demiurgo l’ordinamento del caos iniziale mediante forme e numeri. Eschilo attribuisce la condanna subita da Prometeo per aver quest’ultimo tratto l’uomo dalla condizione selvaggia mediante la conoscenza del numero, “somma fra tutte le scienze”. Ma sarebbe lungo l’elenco di autori antichi e recenti che esaltano l’importanza della matematica. Mi limito a ricordare Sant’Agostino che rivolgendosi a Dio, ripetendo quanto già detto in Sapienza (11, 20), esclama: Tu hai tutto disposto con misura calcolo e peso oppure: Come sono vere e immutabili le regole dei numeri così lo sono quelle della Sapienza.[2]
Veniamo ora alla relazione tra numeri e trinità. Premettiamo solo la circostanza che due insiemi hanno ugual numero di elementi se tra essi vi sia una corrispondenza biunivoca, tale cioè che ad ogni elemento di un insieme ne corrisponda uno ben determinato dell’altro insieme e viceversa.
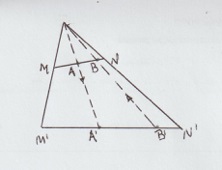
Ad ogni punto A del segmento MN corrisponde il punto A’
di M’N’ e, viceversa, ad ogni punto B’ di M’N’ corrisponde
un punto B di MN. La corrispondente è biunivoca e i due
segmenti, pur di misure diverse, hanno gli stessi punti.
Consideriamo ora l’insieme dei numeri interi 1, 2, 3, 4… e l’insieme dei numeri quadrati 1, 4, 9, 16…. Ebbene, i secondi sono solo una parte dei primi, però, poiché ad ogni numero intero possiamo associare il suo quadrato e ad ogni numero quadrato la sua base, abbiamo una corrispondenza biunivoca che ci porta a stabilire che i due insiemi hanno la stessa numerosità!
Questa circostanza meravigliò Galileo che scrisse un lungo brano a tal proposito, premettendo che si trattava del comportamento dell’infinito che noi non possiamo capire con il nostro intelletto finito. Pertanto, dopo aver ribadito questa nostra impossibilità, si rivolge ai numeri quadrati domandando a Simplicio se essi gli fossero noti:[3]
Simplicio. So benissimo che il numero quadrato è quello che nasce dalla moltiplicazione d’un altro numero in se medesimo: e così il quattro, il nove, etc. son numeri quadrati, nascendo quello da dua e questi dal tre in se medesimi moltiplicati.
Salviati. Benissimo: e sapete ancora, che sì come i prodotti si dimandano quadrati, i producendi, cioè quelli che si multiplicano, si chiamano lati o radici; gli altri poi, che non nascano da numeri multiplicati in se stessi, non sono altrimenti quadrati. Onde se io dirò, i numeri tutti, comprendendo i quadrati e i non quadrati, essere più che i quadrati soli, dirò proposizione verissima: non è così?
Simplicio. Non si può dir altrimenti.
Salviati. Interrogando io di poi, quanti siano i numeri quadrati, si può con verità rispondere, loro esser tanti quante sono le proprie radici, avvenga che ogni quadrato ha la sua radice, ogni radice il suo quadrato, né quadrato alcuno ha più d’una sola radice, né radice alcuna più d’un quadrato solo.
Simplicio. Così sia.
Salviati. Ma se io domanderò, quante siano le radici, non si può negare che elle non siano quante tutti i numeri, poiché non vi è numero alcuno che non sia radice di qualche quadrato; e, stante questo, converrà dire che tutti i numeri quadrati siano quanti tutti i numeri, poiché tanti sono quante le lor radici, e radici son tutti i numeri; e pur da principio dicemmo, tutti i numeri essere assai più che tutti i quadrati, essendo la maggior parte non quadrati
(…)
Simplicio. Che dunque si ha da determinare in questa occasione?
Salviati. Io non veggo che ad altra decisione si possa venire, che a dire, infiniti essere tutti i numeri, infiniti i quadrati, infinite le loro radici, né la moltitudine de’ quadrati essere minore di quella di tutti i numeri, né questa maggiore di quella, ed in ultima conclusione, gli attributi di eguale maggiore e minore non aver luogo ne gl’infiniti, ma solo nelle quantità terminate.
No, come ha detto Simplicio, non si può dire altrimenti,
E quello che è stato detto per i numeri quadrati si può ripetere per i numeri pari (ma anche per altre numerosità) concludendo che se pure i numeri interi sono maggiori sia dei numeri quadrati che di quelli pari essi hanno la loro stessa numerosità.
Abbiamo dunque tre entità: una contenente le altre ma tutte della stessa numerosità. Si tratta del mistero insito nell’infinito come aveva già osservato Dante nel caso della Trinità, spiegata, nel suo mistero appunto dalla matematica, spiegata non come semplice esempio ma come essenza di un problema.
Secondo Pitagora, inoltre, è proprio il numero ad essere divino per cui le due trinità, se avesse conosciuto il problema, sarebbero risultate per lui, azzardiamo questa ipotesi, la stessa cosa. D’altronde sin dai tempi più remoti la matematica era apparsa qualche cosa di misterioso e fecondo al di là dell’uso pratico.
Notiamo infatti che almeno mille anni prima della nascita della Bibbia e di Pitagora, un matematico egizio (Ahmes ?), posto tra il 1800 e il 1500, premette al famoso papiro Rhind[4] la straordinaria premessa ad una matematica ancora rudimentale:
Regole per studiare la natura e per conoscere tutto ciò che esiste, ogni mistero ogni segreto
Silvio Maracchia
[1] Notiamo inoltre che il segmento e la sua sezione aurea sono grandezze tra loro incommensurabili, relazione che difficilmente potrebbe attribuirsi alla divinità con il proprio figlio.
[2] Tutte le citazioni riportate si possono trovare nel mio volume Storia della matematica greca prima di Euclide. Matematica Matematica (ed. Simmetria Roma 2020) consultando ad esempio l’Indice Analitico.
[3] (Discorsi e Dimostrazioni matematiche, Giornata prima. In Galileo. Opere. Salani, , vol. IV, MCMLXIV, pp. 162-164.
[4] 84 problemi di aritmetica, geometria e algebra sviluppati in un papiro di cm 219 x cm 34.




